条件付き確率を求める次の問題について考えてみます。
(例題)
癌の検査の正確さが98%であるとする。つまり、癌にかかっている人がこの検査を受けた場合に、陽性と出る確率が98%であり、癌にかかっていない人が受けた場合には98%の確率で陰性と出る。更に、実際に癌にかかっている人の割合は0.5%程度であるとする。ある人が、この検査を受けたところ、結果は陽性であった。この人が癌にかかっている確率は何パーセントか。
\(P_B(A)=\displaystyle\frac{P(B \cap A)}{P(B)}=\displaystyle\frac{P(A \cap B)}{P(B)}\)
なので、分母分子をそれぞれ計算します(分子は計算するとき意味が分かりやすいようにA,Bを入れ替えました)。なお、\(P(B)\)は陽性と出る確率ですが、癌にかかっている人だけでなく、かかっていない人も陽性と出る場合があります。
(解答)
癌にかかっているという事象をA、陽性と出る事象をBとすると、求める確率は \(P_B(A)\)。
\(P_B(A)=\displaystyle\frac{P(B \cap A)}{P(B)}=\displaystyle\frac{P(A \cap B)}{P(B)}\)
であり、\(P(A \cap B)\) は癌にかかっていて、かつ陽性と出る確率だから
\(P(A \cap B)=\displaystyle\frac{0.5}{100}×\displaystyle\frac{98}{100}=\)\(\displaystyle\frac{49}{100^2}\)
また、癌にかかっていない事象は、\(\overline A\)であり、
\(P(B)=P(A \cap B)+P(\overline A \cap B)\)\(=\displaystyle\frac{0.5}{100}×\displaystyle\frac{98}{100}+\displaystyle\frac{99.5}{100}×\displaystyle\frac{2}{100}\)\(=\displaystyle\frac{248}{100^2}\)
以上より、
\(P_B(A)=\displaystyle\frac{49}{100^2}÷\displaystyle\frac{248}{100^2}=\)\(0.1975・・・\)
だから、\(19.8\)%
・原因の確率
例題では、陽性であったという結果から、癌にかかっているかどうかという原因の確率について考えています。このような確率を原因の確率といい、条件付き確率から求めることができます。例題の設定では検査の結果、陽性であったとき癌である確率は19.8%であり、意外に低いと感じる方も多いではないでしょうか。こうした検査の結果の信頼性を条件付き確率を利用すれば数値で評価できることになります。
・ベイズの定理
例題からも分かりますが、
\(P_B(A)=\displaystyle\frac{P(A \cap B)}{P(B)}=\)\(\displaystyle\frac{P(A \cap B)}{P(A \cap B)+P(\overline A \cap B)}\)・・・①
となります(図を参照してください)。
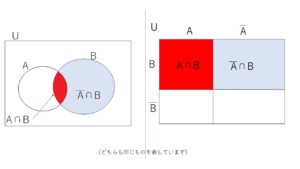
①に確率の乗法定理
\(P(A \cap B)=P(A)P_A(B)\) (\(P(\overline A \cap B)=P(\overline A)P_{\overline A}(B)\))
を代入すると
\(P_B(A)\)\(=\displaystyle\frac{P(A)P_A(B)}{P(A)P_A(B)+P(\overline A)P_{\overline A}(B)}\) ・・・②
であり、②をベイズの定理といいます。
通常の流れとしては、原因があって結果が起こるわけで、A→B の順序になります。②式は B→A の確率を、A→B などの順方向の確率を用いて計算できることを示しています。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。