平行線の性質について見ていきます。
・対頂角、同位角、錯角
次の角の性質があります。
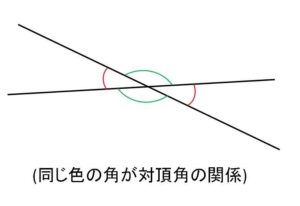
(1)対頂角は等しい
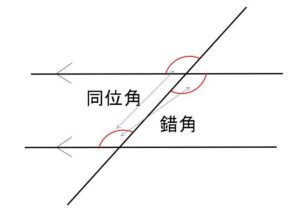
2直線が平行のとき
(2)同位角が等しい
(3)錯角が等しい
また、(2)(3)の逆も成り立つ。つまり同位角または錯角が等しいければ2直線は平行になる。
(解説)
(1)対頂角が等しいのは、隣り合う角の和が\(180°\)であることから分かります。
(2)(3)は対頂角が等しいことを利用すれば同じことを表していて、これらもユークリッドの公準より一応証明はできますが、証明内容はこの公準とほとんど同じなので、(2)(3)は証明できない事実として扱ってよいと思います。
小中高で扱うような図形はユークリッド幾何学とよばれるもので、このユークリッド幾何学で証明できない前提のようなものをユークリッドの公理(公準)といいます。一方、非ユークリッド幾何学という図形の学問も存在し、ユークリッド幾何学の公準が成り立たない部分があるので、図形の性質が変わってきます。例えば曲面上の三角形などで、この三角形の内角の和は\(180°\)になりません。
・三角形の内角の和
三角形の内角の和について次のことが成り立ちます。
(1)3つの内角の和は\(180°\)
(2)1つの外角は、それと隣り合わない2つの内角の和に等しい
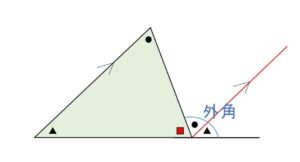
平行線(補助線をひく)の錯角と同位角が等しいことから分かります。
・平行線と線分比
相似を利用すると、平行線に関する線分比が分かります。
(中点連結定理)
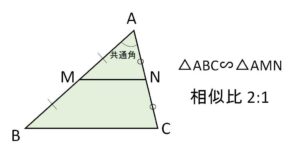
\(△ABC\)において、\(AB,AC\)の中点をそれぞれ\(M,N\)とすると
\(MN//BC\)、\(MN=\displaystyle\frac{1}{2}BC\)
が成り立つ。(逆も成り立つ。つまり上記2条件より\(M,N\)が中点となる)
(一般の線分比)
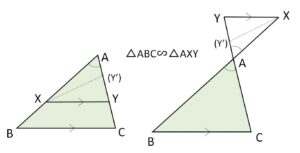
上図で
\(XY//BC⇔AX:AB=AY:AC\)
\(XY//BC⇔AX:XB=AY:YC\)
\(XY//BC→AX:AB=XY:BC\)
(3つ目の逆は必ずしも成り立たず平行にならない場合もある。図の\(Y’\)。2辺とその間の挟む角にならず相似の条件が使えない)
中点連結定理は一般の線分比の特殊例です。これらは平行線の錯角・同位角と相似を利用すれば成り立つことが分かります。
また次のような台形型の線分比では、補助線を引くことにより三角形型の線分比に帰着させます。
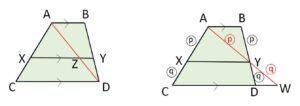
\(AB//CD\) を前提とすると
(1)\(XY\)が\(AB,CD\)に平行ならば、左図より
\(AX:XC=AZ:ZD=BY:YD\) だから
\(AX:XC=BY:YD\)
(2)逆に \(AX:XC=BY:YD\) ならば、右図より
\(AX:XC=BY:YD=AY:YW\ (=p:q)\) だから
\(XY//CD\ (//AB)\)
以上になります。ここまで見て頂きありがとうございました。
next→四角形の種類 back→三角形の合同・相似、三平方の定理