四角形の種類やその特徴についてまとめます。
・四角形の種類
4つの直線で囲まれた図形を四角形といい、4つの辺と4つの頂点をもちます。
四角形はその特徴により、次のように分類されています。
(1)台形:「1組の平行な対辺をもつ」
(2)平行四辺形:「2組の対辺が平行」
(3)ひし形:「4辺の長さが等しい」
(4)長方形:「4つの内角の大きさが全て等しい(すべて直角)」
(5)正方形:「4辺の長さと4つの内角の大きさが等しい(すべて直角)」
(2)平行四辺形については後述するとして、残りについて検討すると
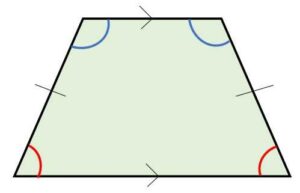
(1)台形:さらに分類すると、底辺(平行な辺からとる)の両端の角の大きさが等しい場合、等脚台形になります。平行でない辺(脚)の長さが等しくなることが名前の由来です。等脚台形は対称的な図形で、2本の対角線の長さが等しいなどの性質をもちます。
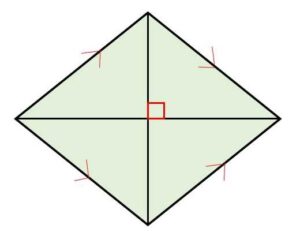
(3)ひし形:2組の対辺が等しい場合には平行四辺形になるので(後述)、ひし形は平行四辺形の特殊例です。また対角線をひくと二等辺三角形が作られ、平行四辺形の対角線は互いに他を2等分することから、ひし形の対角線は垂直に交わることになります。
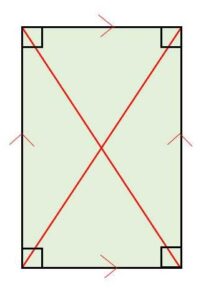
(4)長方形:2組の対角が等しいので、長方形は平行四辺形の特殊例です。また三平方の定理を用いると、2本の対角線の長さが等しいことが分かります。
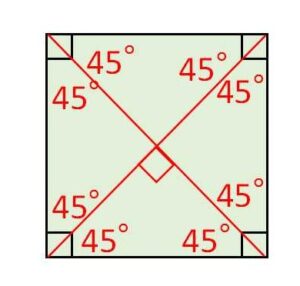
(5)正方形:ひし形でも長方形でもあるので、「2組の対辺は平行、対角線は垂直に交わる、対角線の長さが等しい」という性質をすべてもちます。もちろん平行四辺形の性質ももちます。
しかし、逆が成り立つとは限らないことに注意してください。
例えば
(3)対角線が垂直に交わる→ひし形
(4)対角線の長さが等しい→長方形
は誤りです。
・平行四辺形の性質
平行四辺形:「2組の対辺が平行」・・・①
であることから次の性質がそれぞれ導かれます。また逆に②③④⑤のいずれかが成り立つとき①が導かれるので、②~⑤はいずれも平行四辺形であるための必要十分条件(同値)です。(三角形の合同、錯角や同位角などを利用する)
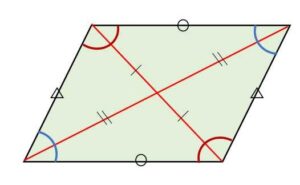
②2組の対辺の長さが等しい
③2組の対角の大きさが等しい
④1組の対辺の長さが等しく、かつ平行
⑤2本の対角線が各々の中点で交わる
問題を解く上で狙われやすいのは④⑤です。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→角の二等分線の定理 back→平行と線分比