角の二等分線の定理について見ていきます。
・内角の二等分線と辺の比
\(△ABC\)の内角の二等分線について次の線分比の定理が成り立ちます。
\(\angle A\) の二等分線と辺\(BC\)の交点を\(P\)とすると、\(P\)は辺\(BC\)を\(AB:AC\)に内分する。
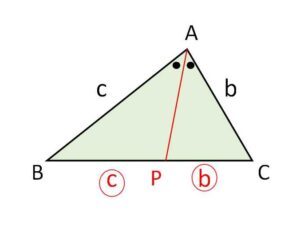
(解説)
単に\(BC\)を\(AB:AC\)に分ける点とすると、辺\(BC\)上にある場合とその延長線上にある場合があるので、これらを内分と外分で区別しています。内角の二等分線の定理では上記の通り\(P\)は内分点であり、後述する外角の二等分線の定理では外分点になります。またこれらの定理は逆も成り立ちますが、これは次回扱いたい思います。
内角と外角は似たような性質をもつことがあり、この線分比の定理はその1例になっています。
なお、もちろん \(\angle B,\angle C\) についても同じことが成り立ちます。
(証明)
平行線になる補助線を引くことで証明が可能です。もしくは面積比を考えてもよいです。
(証明1)補助線
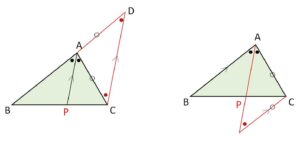
左図について
\(C\)を通り\(AP\)に平行な直線をひき、\(AB\)の延長線との交点を\(D\)とする。
\(\angle\displaystyle\frac{A}{2}=θ\) とすると(図の黒点)
平行線の錯角と同位角により
\(△ACD\)の底角はどちらも\(θ\)になる。
よって\(△ACD\)は二等辺三角形になり
\(AC=AD\)・・・①
また平行線の線分比より
\(AB:AD=BP:PC\)・・・②
①②より
\(AB:AC=BP:PC\)
なお右図のような補助線でも証明可能です。
(証明2)面積比
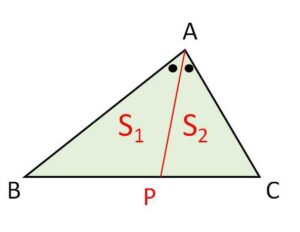
\(\angle \displaystyle\frac{A}{2}=θ\) とすると
\(S_1:S_2\)
\(=\left(\displaystyle\frac{1}{2}\cdot AB \cdot AP\sinθ\right):\left(\displaystyle\frac{1}{2}\cdot AC \cdot AP\sinθ\right)\)
\(AB:AC\)
2つの三角形は高さが共通なので、面積は底辺の長さの比になるから
\(S_1:S_2=BP:PC\)
よって
\(AB:AC=BP:PC\)
・外角の二等分線と辺の比
\(△ABC\)の外角の二等分線について次の線分比の定理が成り立ちます。
\(AB≠AC\) とする。\(\angle A\) の外角の二等分線と辺\(BC\)の延長線との交点を\(P\)とすると、\(P\)は辺\(BC\)を\(AB:AC\)に外分する。
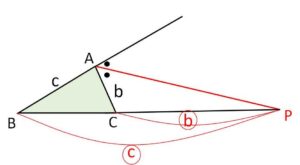
(解説)
\(AB=AC\) だと\(\angle A\)の外角の二等分線と\(BC\)が平行になってしまうので、\(AB≠AC\)という条件がついています。また\(AB,AC\)の大小により外分点\(P\)が右側にある場合と左側にある場合があります。
(証明1)補助線(平行線)
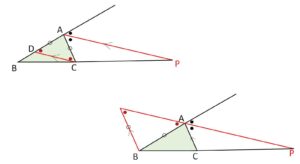
左上図について
\(C\)を通り\(AP\)に平行な直線をひき、\(AB\)との交点を\(D\)とする。
\(\angle A\)の外角の半分を\(θ\)とすると(黒点)、平行線の錯角と同位角により\(△ADC\)の2つの内角は\(θ\)。よって
\(AD=AC\)・・・①
また平行線の線分比により
\(AB:AD=BP:PC\)・・・②
①②より
\(AB:AC=BP:PC\)
なお右図でも証明可能です。
(証明2)面積比
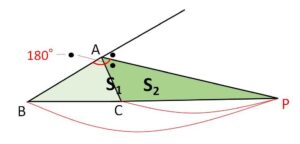
\(△ABP=S_1\)、\(△ACP=S_2\) とする。
\(\angle A\) の外角の半分を\(θ\)とすると(黒点)
\(S_1=\displaystyle\frac{1}{2}AB\cdot AP\sin(180°-θ)\)
\(=\displaystyle\frac{1}{2}AB\cdot AP\sinθ\)
\(S_2=\displaystyle\frac{1}{2}AC\cdot AP\sinθ\)
よって
\(S_1:S_2=AB:AC\)
またこの2つの三角形は高さが共通なので面積と底辺の比は等しく
\(S_1:S_2=BP:PC\)
したがって
\(AB:AC=BP:PC\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→角の二等分線の定理の逆 back→四角形の種類