角の二等分線の定理の逆の成立について見ていきます。
・内角の二等分線の定理の逆
\(△ABC\)において、\(\angle A\) の二等分線と\(BC\)の交点を\(P\)とすると、\(P\)は辺\(BC\)を\(AB:AC\)に内分する点でしたが、この定理の逆も成り立ちます。
\(△ABC\)において、辺\(BC\)を\(AB:AC\)に内分する点を\(P\)とする。このとき\(AP\)は\(\angle A\)の二等分線である。
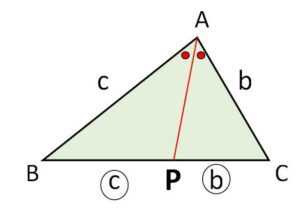
(証明)
もとの定理の証明を応用する方法(平行線と面積比の2つ紹介します)と、同一法があります。
(証明1)平行線の利用
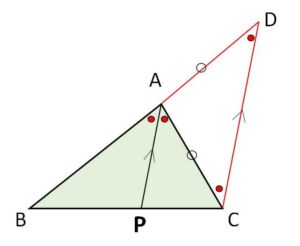
\(C\)を通り\(AP\)に平行な直線を引き、\(AB\)との延長線と交点を\(D\)とする。
平行線の線分比より
\(AB:AD=BP:PC\)・・・①
条件より
\(AB:AC=BP:PC\)・・・②
①②より
\(AD=AC\)
よって\(△ACD\)は二等辺三角形で底角は等しい。(図の赤丸)
したがって平行線の錯角と同位角が等しいことから、図の赤丸の角は等しく
\(AP\)は\(\angle A\)の二等分線となる。
(証明2)面積比の利用
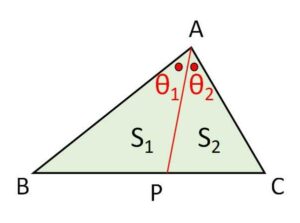
\(S_1:S_2=BP:PC\)
条件より
\(AB:AC=BP:PC\)
よって
\(S_1:S_2=AB:AC\)・・・③
また
\(S_1=\displaystyle\frac{1}{2}AB\cdot AP \sinθ_1\)
\(S_2=\displaystyle\frac{1}{2}AC\cdot AP \sinθ_2\)
だから
\(S_1:S_2=AB\sinθ_1:AC\sinθ_2\)・・・④
③④より
\(\sinθ_1=\sinθ_2\)
(\(θ_1=θ_2\)と結論づけるために、\(θ_1=180°-θ_2\) などを排除するために角の絞り込みをします)
ここで
\(0<θ_1,θ_2<180°\) だから
\(\sinθ_1=\sinθ_2\) を満たすのは
\(θ_1=θ_2\) または \(θ_1=180°-θ_2\)
しかし、\(θ_1+θ_2<180°\) より
\(θ_1<180°-θ_2\) となるから
\(θ_1=180°-θ_2\) は不適。
ゆえに
\(θ_1=θ_2\)
であり、\(AP\)は角の二等分線になる。
(証明3)同一法
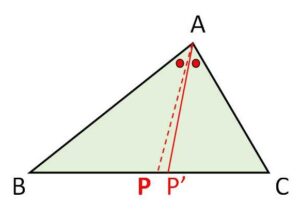
(二等分線を\(AP’\)として、とりあえず\(P,P’\)を別物として扱って一致させます)
\(AP’\)を\(\angle A\)の二等分線とすると、二等分線の定理より\(P’\)は\(BC\)の内分点で
\(AB:AC=BP’:P’C\)・・・⑤
また条件より\(P\)も\(BC\)の内分点で
\(AB:AC=BP:PC\)・・・⑥
⑤⑥より
\(BP’:P’C=BP:PC\)
となるから、\(P\)も\(P’\)も同じ比に\(BC\)を内分する点であり、\(P,P’\)は一致する。
よって\(AP\)も角の二等分線になる。
・外角の二等分線の定理の逆
\(△ABC\)において、\(\angle A\) の外角の二等分線と\(BC\)の延長との交点を\(P\)とすると、\(P\)は辺\(BC\)を\(AB:AC\)に外分する点でしたが、この定理の逆も成り立ちます。
\(△ABC\)において、辺\(BC\)を\(AB:AC\)に外分する点を\(P\)とする。このとき\(AP\)は\(\angle A\)の外角の二等分線である。
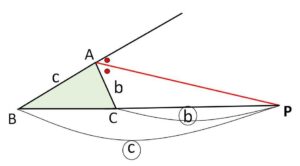
(証明)
内角の場合と同様に証明できます。
(証明1)平行線の利用
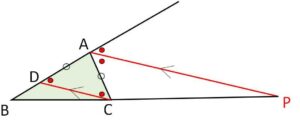
\(C\)を通り\(AP\)に平行な直線を引き、\(AB\)との交点を\(D\)とする。
平行線の線分比より
\(AB:AD=BP:PC\)・・・①
条件より
\(AB:AC=BP:PC\)・・・②
①②より
\(AD=AC\) だから、\(△ADC\)は二等辺三角形。
よって底角(赤丸)は等しく、さらに平行線の同位角と錯角は等しいから、図の赤丸の角は等しい。
よって\(AP\)は外角の二等分線となる。
(証明2)面積比の利用
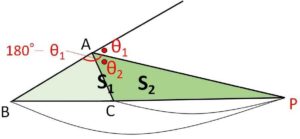
\(△ABP=S_1\)、\(△ACP=S_2\) とおく。
図のように\(θ_1,θ_2\)を設定すると
\(S_1=\displaystyle\frac{1}{2}AB\cdot AP\sin(180°-θ_1)\)
\(=\displaystyle\frac{1}{2}AB\cdot AP\sinθ_1\)
\(S_2=\displaystyle\frac{1}{2}AC\cdot AP\sinθ_2\)
よって
\(S_1:S_2=AB\sinθ_1:AC\sinθ_2\)・・・③
また2つの三角形は高さが共通なので
\(S_1:S_2=BP:PC\)
条件より \(AB:AC=BP:PC\) だから
\(S_1:S_2=AB:AC\)・・・④
③④より
\(\sinθ_1=\sinθ_2\)
ここで
\(0°<θ_1,θ_2<180°\) だから
\(θ_1=θ_2\) または \(θ_1=180°-θ_2\)
しかし \(θ_1+θ_2<180°\) より
\(θ_1<180°-θ_2\) だから
\(θ_1=180°-θ_2\) は不適。
よって \(θ_1=θ_2\)
つまり、\(AP\)は\(\angle A\)の外角の二等分線。
(証明3)同一法
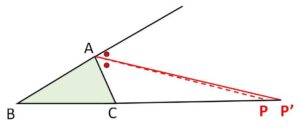
\(\angle A\) の外角の二等分線と\(BC\)の延長との交点を\(P’\)とすると、外角の二等分線の定理より
\(AB:AC=BP’:P’C\)・・・⑤
条件より
\(AB:AC=BP:PC\)・・・⑥
よって⑤⑥より
\(BP’:P’C=BP:PC\)
したがって\(P’\)も\(P\)も\(BC\)の外分点なので、\(P’,P\)は一致し\(AP\)も外角の二等分線となる。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→三角形の辺と角の大小関係 back→角の二等分線の定理