面積比

三角形の面積比と線分比の関係について見ていきます。

・三角形の面積比と線分比
三角形の面積は底辺と高さで決定されるので、2つの三角形について底辺と高さのいずれかが等しければ、もう一方の長さの比が面積比になります。面積比でよく利用されるパターンをまとめると次のようになります。

(等高型)

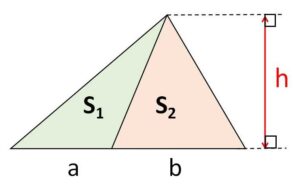
高さが等しければ、面積は底辺の長さの比になります。
\(S_1:S_2=a:b\)

\((S_1+S_2):S_1=(a+b):a\)
\((S_1+S_2):S_2=(a+b):b\)

(等底型)

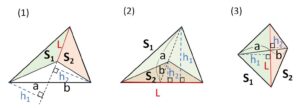
底辺\(L\)が共通なので、面積比は高さの比になります。
高さの比は、平行線の線分比(相似な三角形の辺の比)より
\(h_1:h_2=a:b\) だから
\(S_1:S_2=a:b\)

(等角型)

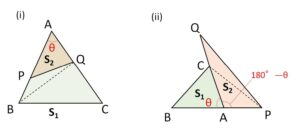
\(△ABC=S_1\)、\(△APQ=S_2\) とする。
(i)では\(θ\)が共通の角なので
\(S_1=\displaystyle\frac{1}{2}AB\cdot AC\sinθ\)
\(S_2=\displaystyle\frac{1}{2}AP\cdot AQ\sinθ\)

よって
\(S_1:S_2=(AB\cdot AC):(AP\cdot AQ)\)

または図のような補助線を引いて、等高型の面積比を2回使ってもよい。

(ii)では共通角は無いが、\(θ\)と\(180°-θ\) に着目して
\(\sinθ=\sin(180°-θ)\)
より、同様に
\(S_1:S_2=(AB\cdot AC):(AP\cdot AQ)\)

または図のような補助線を引いて、等高型の面積比を2回使ってもよい。

(例題)
面積が\(S\)である三角形\(ABC\)の辺\(AB,BC,CA\)上 (ただし両端を除く) に、それぞれ点\(P,Q,R\)をとる。また \(\displaystyle\frac{AP}{AB}=x\)、\(\displaystyle\frac{BQ}{BC}=y\)、\(\displaystyle\frac{CR}{CA}=z\) とおく。

(1)\(x,y,z\)の範囲を求めよ。
(2)三角形\(PQR\)の面積を\(x,y,z\)を用いて表せ。
(3)\(\displaystyle\frac{AP}{AB}+\displaystyle\frac{BQ}{BC}+\displaystyle\frac{CR}{CA}=1\) を満たすとき、三角形\(PQR\)の面積の最大値を\(S\)を用いて表せ。

(解答)
(1)
\(P,Q,R\)はそれぞれ辺上(両端を除く)にあるので
\(0<x<1\)、\(0<y<1\)、\(0<z<1\)

(2)

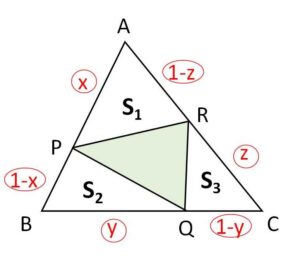
図の\(S_1\)について
\(AB:AP=1:x\)、\(AC:AR=1:(1-z)\) だから、\(△ABC=S\) より
\(S_1=\displaystyle\frac{x(1-z)}{1\cdot1}\cdot S=x(1-z)S\)

同様に
\(S_2=y(1-x)S\)
\(S_3=z(1-y)S\)
となるから

\(△PQR=S-(S_1+S_2+S_3)\)
\(=S-(x+y+z-zx-xy-yz)S\)
\(=(1-x-y-z+xy+yz+zx)S\)

(3)

\(x+y+z=1\)・・・①
だから(2)より
\(△PQR=(xy+yz+zx)S\)・・・②

①より \(z=1-(x+y)\)
よって
\(xy+yz+zx\)
\(=xy+z(x+y)\)
\(=xy+\{1-(x+y)\}(x+y)\)
\(=xy+(x+y)-(x+y)^2\)
(\(x\)について整理して)
\(=-x^2-(y-1)x-y^2+y\)
\(=-\left(x+\displaystyle\frac{y-1}{2}\right)^2+\displaystyle\frac{(y-1)^2}{4}-y^2+y\)
\(=-\left(x+\displaystyle\frac{y-1}{2}\right)^2-\displaystyle\frac{3}{4}y^2+\displaystyle\frac{1}{2}y+\displaystyle\frac{1}{4}\)
\(=-\left(x+\displaystyle\frac{y-1}{2}\right)^2-\displaystyle\frac{3}{4}(y-\displaystyle\frac{1}{3})^2+\displaystyle\frac{1}{3}\)

よって
\(x=-\displaystyle\frac{y-1}{2}\)、\(y=\displaystyle\frac{1}{3}\)・・・③
のとき最大値\(\displaystyle\frac{1}{3}\)をとる。
このとき③より
\(x=\displaystyle\frac{1}{3}\) であり
\(z=1-(x+y)\) より
\(x=y=z=\displaystyle\frac{1}{3}\)

(1)の範囲を満たすので\(△PQR\)の最大値は②より
\(\displaystyle\frac{1}{3}S\)

(別解)

\((x+y+z)^2-3(xy+yz+zx)\)
\(=x^2+y^2+z^2-xy-yz-zx\)
\(=\displaystyle\frac{1}{2}(x-y)^2+\displaystyle\frac{1}{2}(y-z)^2+\displaystyle\frac{1}{2}(z-x)^2≧0\)

よって
\((x+y+z)^2≧3(xy+yz+zx)\)
が成り立ち、等号は\(x=y=z\)のとき成立する。

\(x+y+z=1\) だから
\(1≧3(xy+yz+zx)\)
\(xy+yz+zx≦\displaystyle\frac{1}{3}\)

\(x+y+z=1\)、\(x=y=z\) より
\(x=y=z=\displaystyle\frac{1}{3}\) のとき((1)の範囲内)
\(△PQR=(xy+yz+zx)S\)
は最大値 \(\displaystyle\frac{1}{3}S\) をとる。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→折り返しと最短距離　back→中線定理