折り返しと平面図形

折り返しの平面図形問題です。

 

・折り返しと平面図形

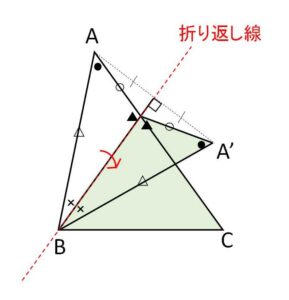
折り返しでは合同な図形(折り返し線について線対称な図形)に着目します。折り返してできた図形は元に戻すとピッタリと元の図形に重なるので合同な図形が現れます。ということは、同じ長さの線分や同じ角度が出現しますが、特に角度が重要です。長方形や正三角形のような図形の折り返しでは、同じ角度が至る所に出現するので、相似であることに着目して問題を解くことになります。

 

 

(例題1)
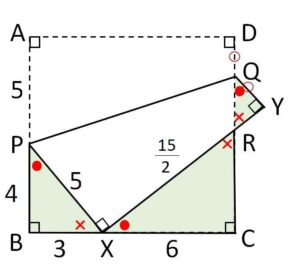
正方形の折り紙\(ABCD\)がある。図のように正方形を折ったあとの頂点\(A,D\)の位置を\(X,Y\)とし、折り目の線を\(PQ\)、\(XY\)と\(CD\)の交点を\(R\)とする。\(X\)はちょうど\(BC\)上にあり、\(BX=3,\ XC=6\) である。

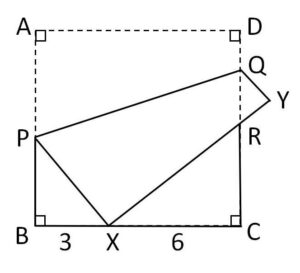
(1)\(PX\)の長さを求めよ。
(2)\(XR\)の長さを求めよ。
(3)\(QD\)の長さを求めよ。

 

(解答)
(1)

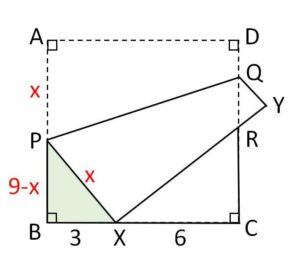
\(PX=x\) とおくと \(PA=x\) となるから、\(△PBX\)において三平方の定理より
\(3^2+(9-x)^2=x^2\)
\(-18x=-90\)
\(x=5\)
よって \(PX=5\)

(2)

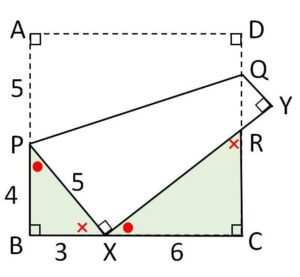
\(\angle BPX+\angle PXB=90°\)・・・①
\(\angle PXY=90°\) だから
\(\angle RXC+\angle PXB=90°\)・・・②
①②より
\(\angle BPX=\angle RXC\) (図の●)
よって1角は直角なので二角相等により
\(△PBX ∽ △XCR\)

(1)の結果からこれらの直角三角形の3辺の比は\(3:4:5\)だから
\(XR=6\cdot\displaystyle\frac{5}{4}\)
\(=\displaystyle\frac{15}{2}\)

(3)

対頂角により
\(\angle XRC=\angle QRY\)
だから、\(△QYR\) も3辺の比が \(3:4:5\) である直角三角形。
よって
\(RY=9-\displaystyle\frac{15}{2}=\displaystyle\frac{3}{2}\)
より
\(QY=\displaystyle\frac{3}{2}\cdot\displaystyle\frac{4}{3}=2\)

\(QY=QD\) だから
\(QD=2\)

 

 

(例題2)
1辺の長さが\(6\)の正三角形\(ABC\)の辺\(BC\)上に点\(P\)があり、\(BP=2\)である。\(A\)を\(P\)に重ねるように\(△ABC\)を折り曲げて、その折り目を\(RS\)とする。

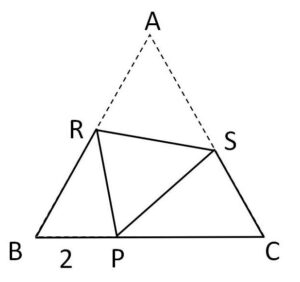
(1)\(RP,PS\)の長さを求めよ。
(2)\(RS\)の長さを求めよ。

 

(解答)
(1)

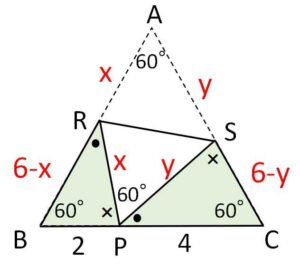
\(60°\)の角に着目すると
\(\angle BRP+\angle BPR=120°\)・・・①
\(\angle SPC+\angle BPR=120°\)・・・②
①②より
\(\angle BRP=\angle SPC\)
よって二角相等により
\(△RBP ∽ △PCS\)・・・③

\(RP=x\)、\(PS=y\) とおけば③より
\(\displaystyle\frac{6-x}{4}=\displaystyle\frac{2}{6-y}=\displaystyle\frac{x}{y}\)

左辺と右辺より
\(y(6-x)=4x\)・・・④
中辺と右辺より
\(x(6-y)=2y\)・・・⑤
④－⑤より\(xy\)を消去して整理すると
\(y=\displaystyle\frac{5}{4}x\)・・・⑥

⑥を④に代入して、\(x≠0\) より
\(\displaystyle\frac{5}{4}(6-x)=4\)
\(x=\displaystyle\frac{14}{5}\)

⑥より
\(y=\displaystyle\frac{7}{2}\)

答 \(RP=\displaystyle\frac{14}{5}\)、\(PS=\displaystyle\frac{7}{2}\)

 

(2)

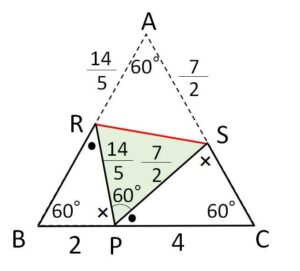
\(△RPS\)において余弦定理より
\(RS=\sqrt{(\displaystyle\frac{14}{5})^2+(\displaystyle\frac{7}{2})^2-2\cdot\displaystyle\frac{14}{5}\cdot\displaystyle\frac{7}{2}\cos60°}\)

\(=\sqrt{49(-\displaystyle\frac{1}{25}+\displaystyle\frac{1}{4})}\)

\(=\displaystyle\frac{7\sqrt{21}}{10}\)

 

 

(例題3)
\(BC=3\)、\(CA=5\) の\(△ABC\)において、辺\(CA\)上に \(\angle BAC=\angle DBC\) となる点\(D\)をとる。辺\(BA\)と\(BD\)が重なるように三角形を折ったときの折り目を\(BE\)、点\(A\)が移った点を\(F\)とする。

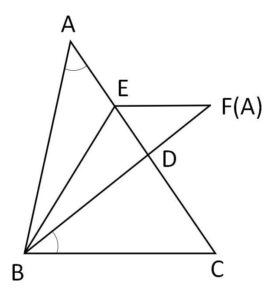
(1)\(△ABC ∽ △BDC\) であることを示せ。
(2)\(CD\)の長さを求めよ。
(3)\(DE\)の長さを求めよ。
(4)\(△DEF\)と\(△ABE\)の面積比を求めよ。

 

(解答)
(1)

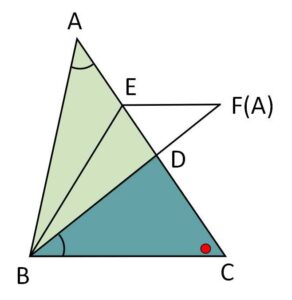
\(\angle BAC=\angle DBC\)、\(\angle C\)が共通だから、二角相等より
\(△ABC ∽ △BDC\)

(2)

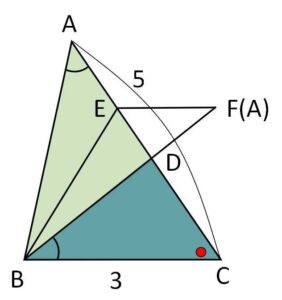
\(AC:BC=BC:CD\) より
\(5:3=3:CD\)
よって \(CD=\displaystyle\frac{9}{5}\)

(3)

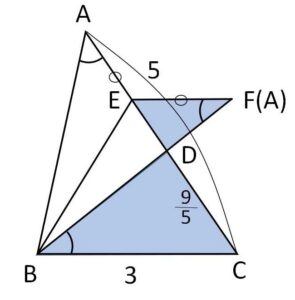
\(\angle DBC=\angle EFD\ (=\angle A)\) より
\(△DBC ∽ △DFE\)　(\(EF//BC\))
また、\(EA=EF\) であるから
\(BC:CD=EF:ED=EA:ED\)
よって
\(EA:ED=3:\displaystyle\frac{9}{5}=5:3\)
\(DA=5-\displaystyle\frac{9}{5}=\displaystyle\frac{16}{5}\) より

\(DE=\displaystyle\frac{16}{5}\cdot\displaystyle\frac{3}{8}=\)\(\displaystyle\frac{6}{5}\)

(4)

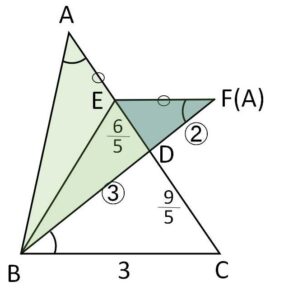
\(△ABE≡△FBE\) だから
\(△DEF\)と\(△ABE\)の面積比は、\(DF\)と\(BF\)の線分の長さの比になる。
\(DF:DB=\displaystyle\frac{6}{5}:\displaystyle\frac{9}{5}=2:3\)
だから
\(DF:BF=2:5\)
よって
\(△DEF:△ABE=2:5\)

 

 

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→折り返しと反射　back→折り返しと最短距離