外心

三角形の外心について見ていきます。

・外心
三角形\(ABC\)において、3辺の垂直二等分線は1点で交わり、その交点は外心とよばれます。

(証明)

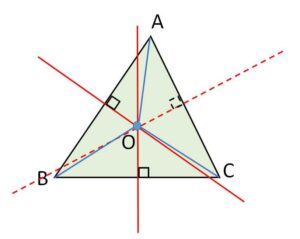
3つの直線は1点で交わるとは限りませんが、2つの直線(平行ではない)は1点で交わるのでこれを利用します。
\(AB,BC\)は平行ではないので、これらの垂直二等分線は交わりその交点を\(O\)とすると
\(OA=OB\)、\(OB=OC\)
よって \(OC=OA\) となるので\(CA\)の垂直二等分線も\(O\)を通り、3つの垂直二等分線は1点\(O\)で交わることになります。

上記証明により
\(OA=OB=OC\)
が成り立つので、\(O\)を中心とする\(A,B,C\)を通る円がかけ、この円を外接円とよびます。

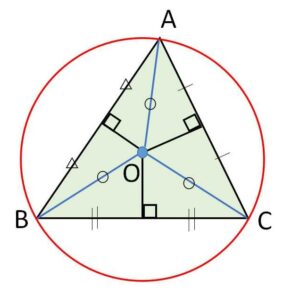
・外心の位置
三角形の種類で外心の位置を分類すると、次のようになります。

鋭角三角形: 三角形の内部
直角三角形: 三角形の辺上
鈍角三角形: 三角形の外部

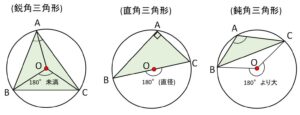
これらのことは\(O\)の位置として「内部・辺上・外部」で網羅していることと円周角の定理(中心角の大きさを考える)を利用して背理法で証明できます。

(例題)
図の\(△ABC\)の外接円の半径\(R\)を正弦定理を利用して求めよ。ただし\(H\)は垂線の足で、\(AB=7\)、\(AC=4\)、\(AH=3\) である。

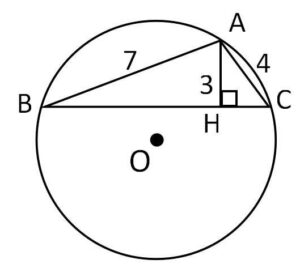
(解答)
正弦定理より
\(2R=\displaystyle\frac{AB}{\sin C}\)
また
\(\sin C=\displaystyle\frac{3}{4}\) だから

\(R=\displaystyle\frac{1}{2}\cdot\displaystyle\frac{7}{\displaystyle\frac{3}{4}}=\)\(\displaystyle\frac{14}{3}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→重心　back→折り返しと反射