重心の性質について見ていきます。
・重心
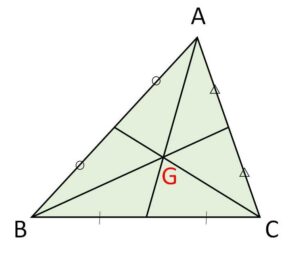
三角形の頂点から対辺の中点へ結んだ線分を中線といいます。各頂点からひいた3つの中線は1点で交わり、この交点は重心と呼ばれます。
(証明1)中点連結定理を利用
線分の中点が現れるので中点連結定理を利用して証明が可能です(要補助線)。
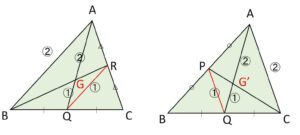
2つの中線ずつで考える。
中線\(AQ,BR\)の左図において、\(QR\)を結ぶと中点連結定理より
\(AG:GQ=2:1\)
中線\(AQ,CP\)の右図において、\(PQ\)を結ぶと中点連結定理より
\(AG’:G’Q=2:1\)
よって\(G,G’\)は一致、つまり\(AQ,BR\)の交点と\(AQ,CP\)の交点が一致するので、3つの中線\(AQ,BR,CP\)は1点で交わる。
なお
\(BG:GR=2:1\)、\(CG:GP=2:1\)
も成り立つので、重心\(G\)は各中線を\(2:1\)に内分している。(下記の性質①)
(証明2)面積比を利用
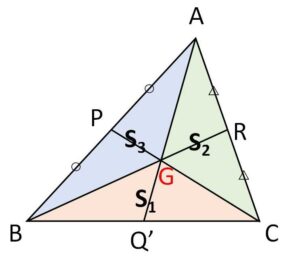
中線\(BR,CP\)の交点を\(G\)とし、\(AG\)を通る直線と\(BC\)の交点を\(Q’\)として、\(AQ’\)が中線であることを示す。
\(P\)は中点なので
\(S_1=S_2\) (等底型)
\(R\)も中点なので
\(S_1=S_3\) (等底型)
よって
\(S_2=S_3\) なので、\(Q’\)も中点。
したがって3つの中線は1点\(G\)で交わる。
・重心の性質
上記証明の中身により、次の重心の性質が分かります。
①重心\(G\)は各中線を頂点の方から\(2:1\)に内分する
②中線によって分けられてできた6つの三角形の面積は全て等しい
(①について)
証明1を利用すれば明らか。
証明2を利用すると
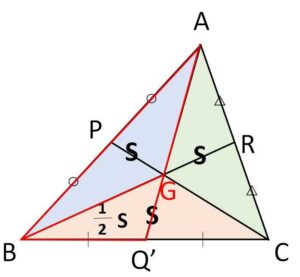
\(S_1=S_2=S_3=S\) とおく。
\(Q’\)は中点なので
\(△GBQ’=\displaystyle\frac{1}{2}S\)
よって
\(AG:GQ’=S:\displaystyle\frac{1}{2}S=2:1\) (等高型)
他の中線も同様。
(②について)
証明1を利用すると
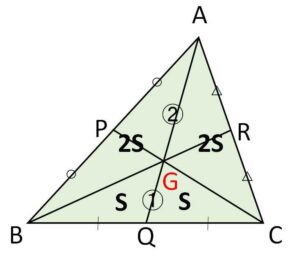
\(Q\)は中点なので
\(△GBQ=△GCQ \ (=S)\)
\(AG:GQ=2:1\) より
\(△GAB=△GAC=2S\)
\(P,R\)も中点だから、6つの三角形の面積は全て\(S\)になり等しい。
証明2を利用すると
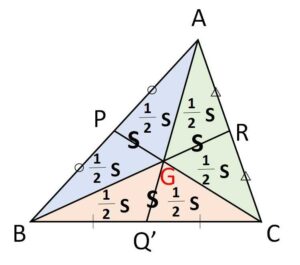
\(S_1=S_2=S_3=S\) とおけば、\(P,Q’,R\)は中点なので6つの三角形の面積は全て\(\displaystyle\frac{1}{2}S\)となることが分かる。
(例題)
\(△ABC\)の辺\(BC,CA,AB\)の中点を\(L,M,N\)とするとき、\(△ABC\)の重心と\(△LMN\)の重心は一致することを示せ。
(解答)
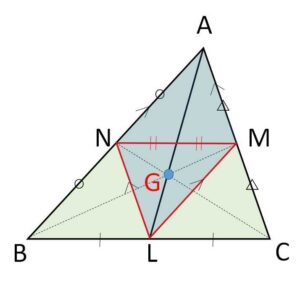
\(△ABC\)の重心を\(G\)とすると、\(G\)は3中線\(AL,BM,CN\)の交点。
中点連結定理により
\(AN//ML\)、\(AM//NL\)
となるから、四角形\(ANLM\)は平行四辺形。
よって平行四辺形の対角線は互いに他を二等分するので
\(AL\)は\(△LMN\)の中線でもある。
同様に\(BM,CN\)も\(△LMN\)の中線であるから、\(G\)は\(△LMN\)の重心となる。
したがって2つの三角形の重心は一致する。