内心の性質について見ていきます。
・内心
三角形の3つの内角の二等分線は1点で交わり、この交点を内心とよびます。
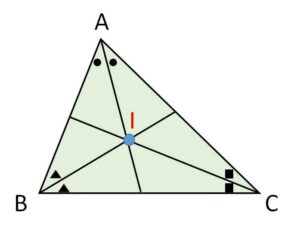
(証明)
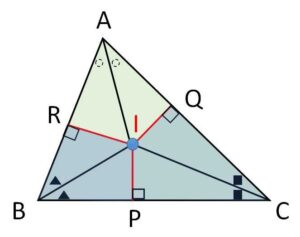
\(\angle B\) と \(\angle C\) の内角の二等分線の交点を\(I\)とする。
\(I\)から各辺に垂線を下ろすと直角三角形の合同(\(\angle B,\angle C\)の箇所)より
\(IR=IP\)、\(IP=IQ\)
よって
\(IR=IQ\)
が成り立つので、\(△ARI≡△AQI\) となり\(AI\)も角の二等分線。
したがって3つの内角の二等分線は一点\(I\)で交わる。
(角の二等分線が、角をつくる2辺から等距離にある点の集合であることを利用してもよい。ただしこれも三角形の合同から分かることなので実質的に同じ。)
また
\(IP=IQ=IR \ (=r)\)
とこれら3つの線分は辺の1つと垂直であることから、\(I\)を中心とする半径\(r\)の円は\(P,Q,R\)で辺と接する円になります。この円を内接円とよびます。
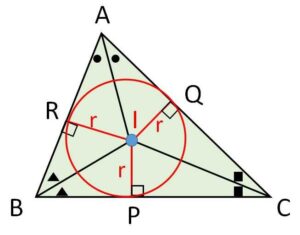
なお一般的には、角の二等分線上には内接円の接点は無いことに注意してください。例えば\(AI\)は二等辺三角形のような特殊な事情が無い限り\(P\)を通りません。
・内心の性質
内心のよく利用する性質をまとめておきます。
①面積と内接円の半径\(r\)の関係
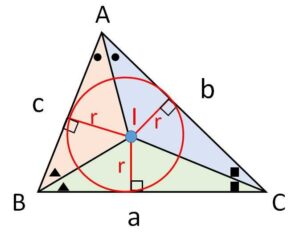
\(△ABC\)の面積を\(S\)とすれば、高さ\(r\)の3つの三角形の和を考えて
\(S=\displaystyle\frac{1}{2}r(a+b+c)\)
3辺の長さ\(a,b,c\)が分かっていれば「余弦定理→正弦へ変換」or「ヘロンの公式」で面積が求まるので内接円の半径\(r\)が求まる算段です。
②内心が作る角
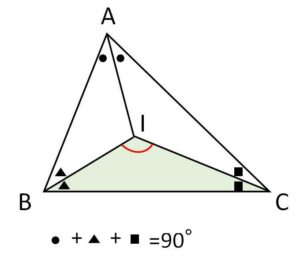
\(\angle A+\angle B+\angle C=180°\) より
\(\displaystyle\frac{1}{2}\angle A+\displaystyle\frac{1}{2}\angle B+\displaystyle\frac{1}{2}\angle C=90°\)
よって\(△IBC\)に着目すると
\(\angle BIC=180°-(\displaystyle\frac{1}{2}\angle B+\displaystyle\frac{1}{2}\angle C)\)
\(=180°-(90°-\displaystyle\frac{1}{2}\angle A)\)
\(=90°+\displaystyle\frac{1}{2}\angle A\)
同様に
\(\angle CIA=90°+\displaystyle\frac{1}{2}\angle B\)
\(\angle AIB=90°+\displaystyle\frac{1}{2}\angle C\)
③内心と外接円
例題参照
(例題)
\(△ABC\)の内心を\(I\)とし、\(AI\)の延長が外接円と交わる点を\(D\)とすると
\(DB=DC=DI\)
であることを示せ。
(解答)
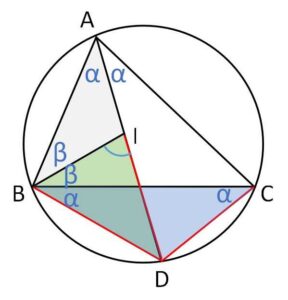
\(AI\)は内角の二等分線で、円周角の定理を用いると図の\(α\)は全て同じ角。
よって\(△DBC\)は二等辺三角形だから
\(DB=DC\)・・・①
また\(BI\)も内角の二等分線だから図の\(β\)は等しい角。よって2内角の和は残りの角の外角になるから図より
\(\angle DBI=\angle DIB=α+β\)
ゆえに\(△DBI\)も二等辺三角形で
\(DB=DI\)・・・②
したがって①②より
\(DB=DC=DI\)