オイラー線について見ていきます。
・オイラー線
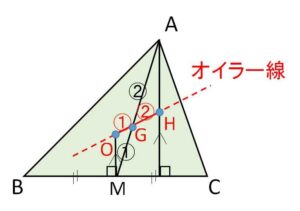
正三角形でない三角形の外心\(O\)・重心\(G\)・垂心\(H\)は一直線上にあり、この3点を通る直線をオイラー線とよびます。また重心は、外心と垂心を結ぶ線分を外心のほうから\(1:2\)に内分します。つまり、\(OG:GH=1:2\) です。
正三角形ではこれら3点(内心も含めると4点)は一致し(後述)、これら(1点)を通る直線は無数にあるためオイラー線は定義されません。
(証明)
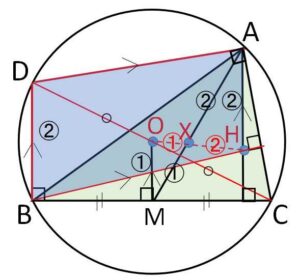
外接円との関連性を意識して、\(C\)を通る直径\(CD\)をベースに補助線を引きます。証明の流れは
「平行四辺形の発見→平行線の相似形に着目→重心の位置の把握」です。
\(CO\)と外接円の交点を\(D\)とし、\(DB,DA\)を結ぶ。
\(CD\)が外接円の直径であることに注意すると、\(DB,AH\)はどちらも\(BC\)に垂直だから
\(DB//AH\)・・・①
また\(DA,BH\)は\(AC\)に垂直だから
\(DA//BH\)・・・②
①②より四角形\(DBHA\)は平行四辺形だから
\(DB=AH\)・・・③
次に\(△CDB\)において中点連結定理より
\(DB=2OM\)・・・④
③④より
\(2OM=AH\)・・・⑤
\(OM\)は\(BC\)の垂直二等分線だから
\(OM//AH\)・・・⑥
よって\(AM\)と\(OH\)の交点を\(X\)とすれば⑤⑥より
\(X\)は中線\(AM\)を\(2:1\)に内分する点だから、\(X\)は重心\(G\)である。よって\(O,G,H\)は一直線上にある。また
\(OG:GH\ (=OX:XH)\ =1:2\)
だから、\(G\)は\(OH\)を\(1:2\)に内分する点となる。
・正三角形の五心(傍心除く)
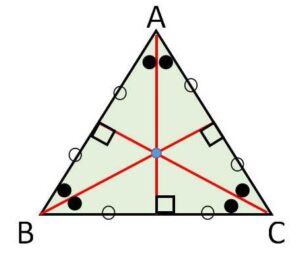
正三角形では、外心・重心・垂心・内心は一致します。理由は頂点から引いた中線が、内角の二等分線・垂直二等分線でもあるからです。
なお、逆にこれら4つの点のうちいずれかの2点が一致すれば正三角形になります(残りの2点も自動的に一致する)。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→チェバの定理 back→傍心