メネラウスの定理について見ていきます。
・メネラウスの定理
三角形と直線に関する線分比の次の定理が成り立ちます。
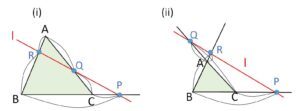
\(△ABC\)と頂点を通らない直線\(l\)がある。辺\(BC,CA,AB\)またはその延長と\(l\)が交わるとき、その交点を\(P,Q,R\)とすると
\(\displaystyle\frac{BP}{PC}\cdot\displaystyle\frac{CQ}{QA}\cdot\displaystyle\frac{AR}{RB}=1\)
(解説)
分数の分母が\(0\)にならないように、頂点を通らないという条件がついています。
直線\(l\)のとりかたとしては
(i)三角形の辺と交わる(交点は辺上2個と延長上1個)
(ii)三角形の辺と交わらない(交点は延長上3個)
の場合があり図は異なりますが、結果と証明方法は同じです。結果の分数式も、その覚え方も「頂点→中継(分点)→頂点→中継(分点)→」の繰り返しでチェバの定理と同じです。
(証明1)垂線を下ろす
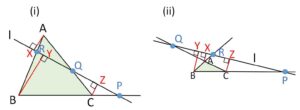
頂点から直線\(l\)に垂線を下ろし、線分の長さの比を垂線の長さの比に変換します。
3垂線は平行なので
\(\displaystyle\frac{BP}{PC}=\displaystyle\frac{BY}{CZ}\)
\(\displaystyle\frac{CQ}{QA}=\displaystyle\frac{CZ}{AX}\)
\(\displaystyle\frac{AR}{RB}=\displaystyle\frac{AX}{BY}\)
辺々掛けると
\(\displaystyle\frac{BP}{PC}\cdot\displaystyle\frac{CQ}{QA}\cdot\displaystyle\frac{AR}{RB}=1\)
(証明2)平行線を利用
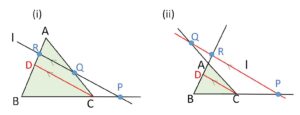
(線分比をすべて\(AB\)上に移します)
\(C\)を通り\(l\)に平行な直線をひき、\(AB\)との交点を\(D\)とする。
\(CD//l\) より
\(\displaystyle\frac{BP}{PC}=\displaystyle\frac{BR}{RD}\)・・・①
\(\displaystyle\frac{CQ}{QA}=\displaystyle\frac{RD}{AR}\)・・・②
よって
\(\displaystyle\frac{BP}{PC}\cdot\displaystyle\frac{CQ}{QA}\cdot\displaystyle\frac{AR}{RB}\)
\(=\displaystyle\frac{BR}{RD}\cdot\displaystyle\frac{RD}{AR}\cdot\displaystyle\frac{AR}{RB}\)
\(=1\)
(例題1)
\(△ABC\)において、辺\(BC\)上に \(BP=\displaystyle\frac{1}{3}BC\) を満たす点\(P\)をとり、辺\(AB\)上に \(AQ=\displaystyle\frac{1}{3}AB\) を満たす点\(Q\)をとる。\(AP\)と\(CQ\)の交点を\(T\)とするとき、\(△ABC\)の面積は\(△AQT\)の面積の何倍か。
あとは三角形の面積比(等高・等角)を求めるだけです。
(解答)
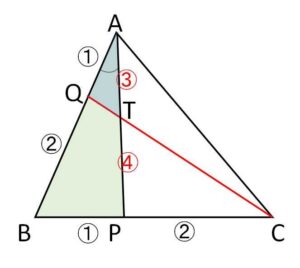
\(△ABP\)と\(QC\)においてメネラウスの定理より
\(\displaystyle\frac{3}{2}\cdot\displaystyle\frac{PT}{TA}\cdot\displaystyle\frac{1}{2}=1\)
よって
\(\displaystyle\frac{PT}{TA}=\displaystyle\frac{4}{3}\)
\(△ABC=S\) とおくと
\(△ABP=\displaystyle\frac{1}{3}S\) だから
\(△AQT=\displaystyle\frac{1}{3}\cdot\displaystyle\frac{3}{7}△ABP\)
\(=\displaystyle\frac{1}{21}S\)
したがって\(21\)倍。
(例題2)
\(△ABC\)の内部の点を\(O\)とし、\(AO,BO,CO\)の延長が対辺と交わる点をそれぞれ\(D,E,F\)とする。\(E,F\)を通る直線をひき、この直線が辺\(BC\)の延長と交わるときその交点を\(G\)とする。このとき \(\displaystyle\frac{BD}{DC}=\displaystyle\frac{BG}{GC}\) を示せ。(チェバの定理も併用せよ)
(解答)
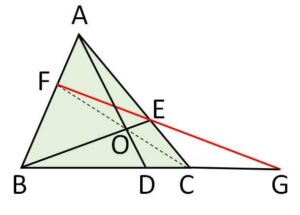
\(△ABC\)でチェバの定理より
\(\displaystyle\frac{BD}{DC}\cdot\displaystyle\frac{CE}{EA}\cdot\displaystyle\frac{AF}{FB}=1\)
よって
\(\displaystyle\frac{BD}{DC}=\displaystyle\frac{EA}{CE}\cdot\displaystyle\frac{FB}{AF}\)・・・①
また\(△ABC\)と直線\(FG\)でメネラウスの定理より
\(\displaystyle\frac{BG}{GC}\cdot\displaystyle\frac{CE}{EA}\cdot\displaystyle\frac{AF}{FB}=1\)
よって
\(\displaystyle\frac{BG}{GC}=\displaystyle\frac{EA}{CE}\cdot\displaystyle\frac{FB}{AF}\)・・・②
①②の右辺は同じだから
\(\displaystyle\frac{BD}{DC}=\displaystyle\frac{BG}{GC}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→チェバ・メネラウスの定理の逆 back→チェバの定理