円の接線

円と直線の関係について見ていきます。

・円と直線
円と直線の位置関係は次の3パターンに分類されます。

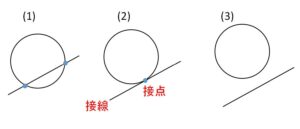
(1)2点で交わる。
(2)1点で交わる。(接する)
(3)交わらない。

特に(2)の直線は接線、1交点は接点とよばれます。

・円の接線と垂直
円の接線と中心と接点を結ぶ直線の関係は次の通りです。

(円の接線と垂直)
①中心を\(O\)とする円の接線\(l\)が\(T\)で接している。このとき\(OT \perp l\)。
②逆に円周上の\(T\)を通る直線\(l\)が、\(OT \perp l\) を満たすならば、\(l\)は接線である。

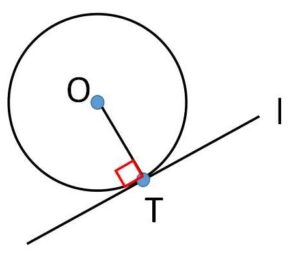
(解説)
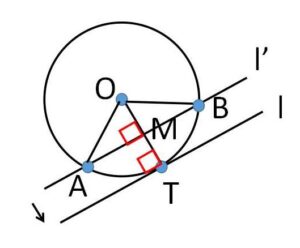
円の接線と垂直に関する基本かつ重要な定理です。接点\(T\)を通り接線\(l\)に垂直な直線(法線)が円の中心\(O\)を通るともいえます。①については、下図で2交点で交わる直線\(l’\)を2交点\(A,B\)が近づくように動かして1点\(T\)で接するように考えると、\(A,B\)の中点\(M\)と直線\(l’\)がそれぞれ\(T,l\)に近づき、また \(OM \perp l’\) なので \(OT \perp l\) であることが分かります。丁寧に証明すると次の通りです。

(証明)
(背理法を利用する)
①については

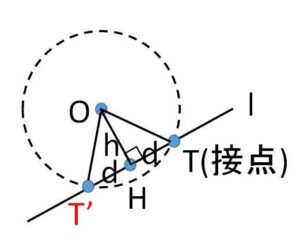
\(OT\)と\(l\)が垂直でないと仮定すると、\(OH \perp l\) を満たす\(T\)とは異なる\(H\)を\(l\)上にとることができる。また\(H\)について反対側に \(HT=HT’\ (=d)\) となる\(T’\)もとれる。このとき\(OH=h\)とすると、三平方の定理より \(OT=OT’\ (=\sqrt{d^2+h^2})\) となるから、\(O\)を中心とする\(T\)を通る円は\(T’\)も通り、\(l\)はこの円と2交点で交わるので\(l\)が接線であることに矛盾。したがって \(OT \perp l\)。

②については

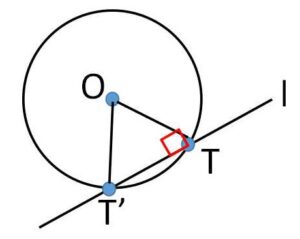
\(l\)が円と2点で交わると仮定する(\(T\)は通るので交点なしは考えなくてよい)。もう1つの交点を\(T’\)とすると、\(△OTT’\)は二等辺三角形。よって \(OT \perp l\) だから
\(\angle OTT’=\angle OT’T=90°\)
すると\(△OTT’\)の内角の和が\(180°\)を超えるので矛盾。よって\(l\)は接線である。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→内接四角形の定理　back→円周角の定理の逆・円の外部内部と円周角