幾何的性質を利用した軌跡・領域についてです。
・軌跡(領域)
ある軌跡や領域を求める際には「座標 や ベクトル」を利用することが基本ですが、幾何を利用しても求まる場合があります。その基本形をまとめておきます。
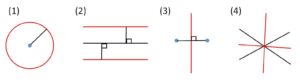
(1)円1
→定点から一定の距離の点の軌跡
(2)平行な直線
→定直線から一定の距離の点の軌跡
(3)垂直二等分線
→2定点からの距離が等しい点の軌跡
(4)角の二等分線
→2定直線からの距離が等しい点の軌跡
(5)円2(弧)
→定線分を見込む角が一定である点の軌跡(円周角の定理の逆)
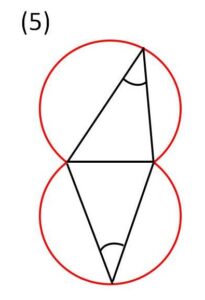
特に(5)が重要です。またいずれにおいても軌跡の形が決まってもその全体を動くかどうかの確認は必要です。(十分性を確かめる)
(例題1)
正三角形\(ABC\)の2辺\(AB,AC\)上にそれぞれ動点\(D,E\)が、\(AD=CE\)となるように移動する。
(1)\(△ADC≡△CEB\)を示せ。
(2)\(BE,CD\)の交点\(P\)の軌跡を求めよ。
(解答)
(1)
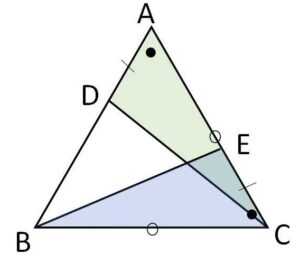
仮定より \(AD=CE\)
また\(△ABC\)は正三角形だから
\(AC=CB\)、\(\angle CAD=\angle BCE\)
よって、2辺とはさむ角が等しいので
\(△ADC≡△CEB\)
(2)
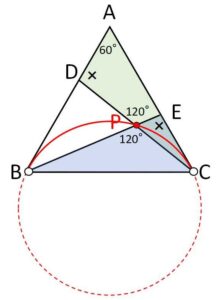
(1)より \(△ADC≡△CEB\) だから
\(\angle ADC=\angle CEB\)
よって四角形\(ADPE\)は円に内接するので
\(\angle DPE=180°-60°=120°\)
ゆえに対頂角は等しいので
\(\angle BPC=120°\)
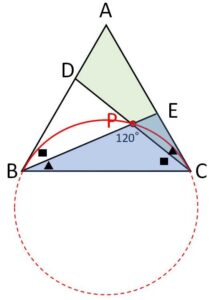
\(BC\)は定線分だから、\(P\)は\(BC\)を見込む角が\(120°\)となるような円弧上にある。ただし、\(P\)は線分\(BE,CD\)の交点だから\(△ABC\)の内部にあり、\(D,E\)が動くことを考慮すると、図の円弧\(BC\)が求める軌跡(端点を除く)。
(注)
軌跡の円(弧)は\(AB,AC\)に接します。
(1)の合同な三角形と、\(\angle B,\ \angle C\) が\(60°\)であることから下図の角▲,■が等しくなり、接弦定理の逆より接線になることが分かります。
(例題2)
直線\(l\)上に3点\(A,B,C\)をこの順にとり、\(AB\)を直径とする円を\(O\)とする。\(C\)を通る直線\(m\ (≠l)\) を円\(O\)の円周と2点で交わるように引き、\(C\)に近い交点を\(B’\)とし、他の交点を\(A’\)とする。\(AA’\)と\(BB’\)の交点を\(P\)とし、\(AB’\)と\(BA’\)の交点を\(Q\)、\(PQ\)と\(l\)の交点を\(R\)とする。
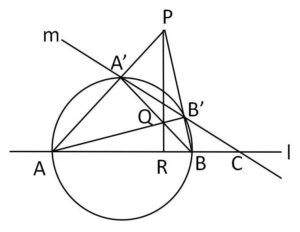
(1)\(\displaystyle\frac{AR}{RB}=\displaystyle\frac{AC}{CB}\) が成り立つことを証明せよ。
(2)直線\(PR\)は\(l\)に垂直であることを証明せよ。
(3)直線\(m\)が上の条件を満たしながら動くときの、点\(P\)の軌跡を求めよ。
(解答)
(1)
(目的の式が得られるように、チェバとメネラウスの定理を利用します)
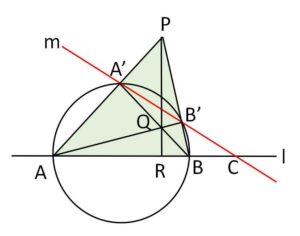
チェバの定理より
\(\displaystyle\frac{AR}{RB}\cdot\displaystyle\frac{BB’}{B’P}\cdot\displaystyle\frac{PA’}{A’A}=1\)・・・①
メネラウスの定理より
\(\displaystyle\frac{AC}{CB}\cdot\displaystyle\frac{BB’}{B’P}\cdot\displaystyle\frac{PA’}{A’A}=1\)・・・②
よって①②より
\(\displaystyle\frac{AR}{RB}=\displaystyle\frac{AC}{CB}\)
(2)

\(AB\)は円の直径なので
\(\angle AA’B=\angle AB’B=90°\)
よって\(Q\)は垂心となるから
\(PR \perp l\)
(3)
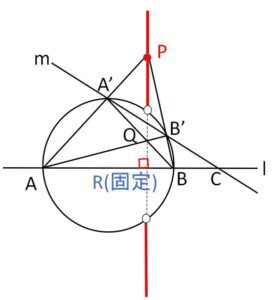
(1)の結果
\(\displaystyle\frac{AR}{RB}=\displaystyle\frac{AC}{CB}\)
と\(A,B,C\)が定点であることから、\(R\)は線分\(AB\)を\(AC:CB\)に内分する定点である。
よって(2)より、\(P\)は\(R\)を通り\(l\)に垂直な直線上にあるが、問題の設定により円の内部と周上に\(P\)はない。また\(m\)を動かすと、この垂直な直線上の円の外部にある部分を\(P\)はくまなく動く。したがって求める軌跡は「線分\(AB\)を\(AC:CB\)に内分する点\(R\)を通り\(l\)に垂直な直線のうち、円\(O\)の外部にある部分」
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→オイラーの定理(内心と外心の定理) back→接する複数の円