2円の位置関係

2円の位置関係と共通接線についてまとめておきます。

 

・2円の位置関係
2円の中心間距離\(d\)に着目すると、次のように2円の位置関係を分類できます。(ただし2円の半径\(r,r’\)を異なるものとし、\(r>r’\)とします。2円の半径が同じ場合は各所で補足します)

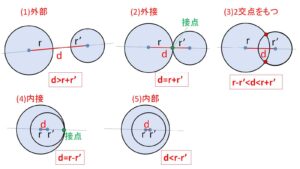
図より\(d\)と\(r+r’,\ r-r’\)の大小関係で5つのグループに分類できます。(3)は(2)(4)の間、(5)は(4)より小さい\(d\)となっています。

(1)~(5)より2円の交点の個数は(3)2個、(2)(4)1個、(1)(5)0個(共有点なし)の3種類になりますが、1個の場合2円は接するといい、特に(2)外部で接する場合は外接、(4)内部で接する場合は内接とよびます。いずれも接点は2円の中心を結んだ直線上にあることは重要な性質です。これは円の対称性から分かります。(2円の中心を結んだ直線は直径と重なることから、この直線について2円は対称。よってもし接点がこの直線上に無いと2個交点をもってしまう)

また2円の半径が等しい場合は(1)~(3)については同様ですが、(4)(5)の場合はなく代わりに2円全体が重なる(一致する)という場合が出てきます。

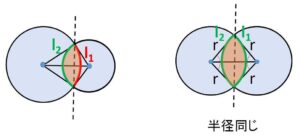
なお(3)のケースについてですが、一般に互いに切り取られる円弧のそれぞれの長さ\(l_1,l_2\)は等しくはないですが、2円の半径が等しい場合には中心角と半径が同じであることから等しくなります。同様に2交点を結ぶ直線は2円の共通部分を一般的には2等分しませんが、半径が等しい場合には2等分します。

 

 

・共通接線
2円のいずれにも接する接線(共通接線)の本数を、上記5グループで検討すると次のようになります。

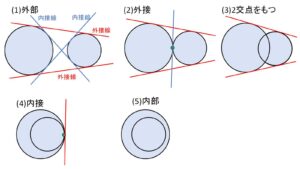
(1)計4本 (共通外接線2本、共通内接線2本)
(2)計3本 (共通外接線2本、共通内接線1本)
(3)計2本 (共通外接線2本)
(4)計1本 (共通外接線1本)
(5)なし

2円が接線について同じ側にあるときこの接線を共通外接線、反対側にあるときこの接線を共通内接線とよびます。

 

 

 

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→共通接線の長さ　back→トレミーの定理