球が接する例題です。
球同士が接する場合には、中心間を線分で結びその線分上に接点があることを利用するのが基本です。また断面図を考える場合には、球の中心や接点を含む平面を取り出します。
(例題)
\(4\)つの半径\(3\)の球が互いに外接しながら円柱に内接している。
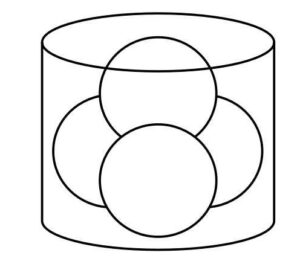
(1)円柱の高さを求めよ。
(2)円柱の底面の半径を求めよ。
(解答)
(1)
上下面で接することから決定します。上に乗っている球は下の球の隙間に入りこんでいるので、単純に球の直径の2倍が高さになりません。基本通りに球の中心間を線分で結ぶと、正四面体ができることから、この正四面体の高さを利用して求まることになります。
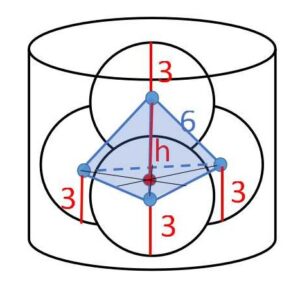
4つの球の中心を結んでできる正四面体の高さは
\(h=\sqrt{6^2-(\displaystyle\frac{2}{3}\cdot3\sqrt{3})^2}\)
\(=2\sqrt{6}\)
よって円柱の高さは
\(3+2\sqrt{6}+3=\)\(6+2\sqrt{6}\)
(2)
使っていない側面に接する条件を利用します。底面に平行に切断した場合に最も球の切断面の円の半径が大きくなるように、球の中心を通るように切断します。この切断面上に円柱との接点があり、円は互いに接しています。
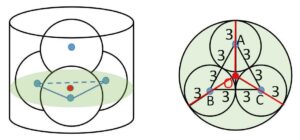
円柱の底面に平行な、下側の3つの球の中心を通る平面での断面を考える。
断面において外側の円の中心を\(O\)、半径を\(r\)とすれば
\(OA=OB=OC=r-3\)
となるので、\(O\)は\(△ABC\)の外心であり、\(△ABC\)が正三角形であるから重心でもある。\(r\)は底面の円の半径であり
\(OA=\displaystyle\frac{2}{3}\cdot3\sqrt{3}=2\sqrt{3}\) より
\(r=3+OA\)
\(=3+2\sqrt{3}\)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→対称性のある立体 back→球の性質