・直線と平面の位置関係
空間において、直線と平面の位置関係は次の3パターンに分類されます。
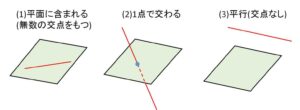
よく使うのが(1)で、2点がある平面に含まれるとき、その2点を通る直線上の点はすべてこの平面に含まれることになります。
・直線と平面の垂直
直線と平面の垂直は次のように定義されます。
直線\(l\)が平面\(α\)上のすべての直線に垂直であるとき、直線\(l\)と平面\(α\)は垂直であるといい、\(l \perp α\) とかく。
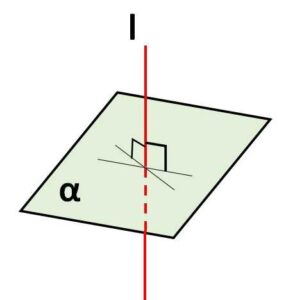
逆に\(l \perp α\) であるとき、直線\(l\)と平面\(α\)上の任意の直線は垂直です。
ところで、すべての直線について垂直であることを調べるのは大変なので、次の定理を利用して2本の直線についてだけ調べることになります。
直線\(l\)が平面\(α\)上の交わる2直線に垂直ならば、\(l \perp α\) である。
(解説)
2本の直線に垂直であるという条件が必要です。\(α\)上の2直線が平行だと実質1本のみの直線と垂直になるので、交わる2直線という文言がついています。証明は二等辺三角形の性質(中線が底辺と垂直)を利用するために、\(α\)について対称な図形を考えます。
(証明)
仮定より\(l\)が\(α\)上の2直線\(m,n\)に垂直なので、\(l\)と\(α\)は1交点\(O\)をもつ。
ここで\(α\)上の2直線\(m,n\)の交点が\(O\)であるときを考えればよい。(交点が\(O\)でない場合は平行移動させる)
また同様の理由で、\(O\)を通る\(m,n\)以外の\(α\)上の任意の直線\(u\)について考えればよい。
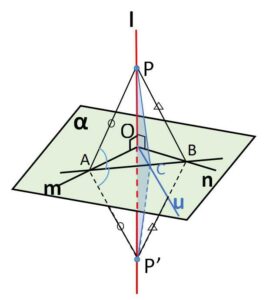
(目標は\(u\)と\(l\)の垂直です。二等辺三角形を作るためにもう少し設定をします)
\(l\)上に\(α\)について対称となる点\(P,P’\)をとると、\(O\)は線分\(PP’\)の中点。
また\(O\)を通らない直線\(m,n,u\)と交わる直線を引き、交点をそれぞれ\(A,B,C\)とする。
\(l \perp m,l \perp n\) と\(O\)が\(PP’\)の中点であることから
\(△APP’\)と\(△BPP’\)は二等辺三角形。
よって、\(AP=AP’,\ BP=BP’\) となるから、\(AB\)が共通であることも合わせると
\(△PAB≡△P’AB\)
ゆえに \(\angle PAC=\angle P’AC\) だから、二辺夾角相等より
\(△PAC≡△P’AC\)
よって\(△CPP’\)は二等辺三角形だから、\(O\)が\(PP’\)の中点であることから
\(l \perp u\)
したがって、\(l\)と\(α\)上の任意の直線は垂直になるので、\(l \perp α\) となる。
・直線と平面のなす角
一般的な平面と直線のなす角は次のように定めます。
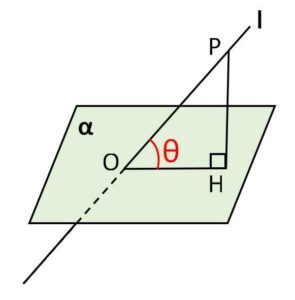
\(l \perp α\)でないとする。直線\(l\)と平面\(α\)が1点\(O\)で交わるとき、\(l\)上の点\(P\)(\(O\)は除く)から\(α\)に垂線\(PH\)を下ろす。このとき、\(\angle POH=θ\) (\(0°<θ<90°\)) を直線\(l\)と平面\(α\)のなす角という。なす角は大きい角と小さい角の2種類が考えられますが、通常は小さい方の角(鋭角)をとります。
(平行または平面に含まれる場合には、なす角は\(0°\)とする。また、\(l \perp α\) のときはなす角は\(90°\)とする。)
・垂直二等分面
今回のメインテーマではありませんが、重要な内容なのでここで扱っておきます。
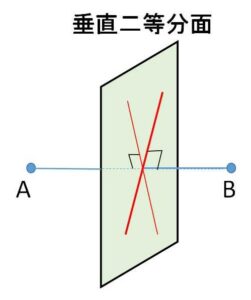
平面において2点から等距離である点の集合は垂直二等分線でしたが、空間において2点から等距離である点の集合は垂直二等分面になります。これは2点\(A,B\)を通るある平面を考えると、この平面上では等距離の点の集合は垂直二等分線になり、\(A,B\)を通る平面は無数にあるので、これらを平面を回転させるようにして考えることにすると、これに伴い垂直二等分線が回転して垂直二等分面になることが分かります。
以上になります。お疲れ様です。
ここまで見て頂きありがとうございました。
next→空間図形の基本③(2平面) back→空間図形の基本①(2直線)