立体の断面

立体の断面についてです。

・立体の断面(平面立体)
立体の断面を考える場合、頭の中や図で断面を考えることも大事ですが、機械的な手法があればその方法をマスターするのも問題を解く上で便利です。とくに立方体や直方体のような、平面で作られた立体で平行面をもつものは次のようなルールで断面を考えることができます。

(解説)
(1)について

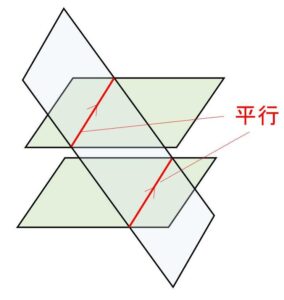
平行な2平面を3つ目の平面で切ると、その切断面である交線は平行となり、このことを利用すれば対面の切断面を調べることができます。
(1)が成り立つ理由は、2交線は平行な平面のそれぞれにあるので交わらないことと、2交線はいずれも第3の平面上にもあり同一平面にあることから分かります。(空間ではねじれの可能性もあるが、同一平面上で交わらない2直線は平行)

(2)~(4)について
具体例を挙げて説明します。

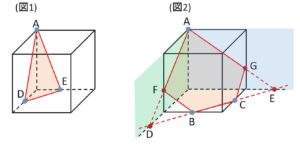
(4)は基本理念であることとして、上図のような立方体の切断面について考えます。

(図1)で、3点\(A,D,E\)を通る平面(同一直線上にない3点なので平面が1つに決まる)で立方体を切断する場合その断面図は、\(A,D\)、\(D,E\)、\(A,E\)がそれぞれ同じ立方体の面にあるのでこれらを結ぶだけで切断面である三角形を図示することができます。

一方(図2)で、3点\(A,B,C\)を通る平面で立方体で切断する場合は\(BC\)は結ぶとしてもこのままだと手詰まりです。(1)を使うにしても\(BC\)に平行な\(A\)を通る直線を考えても立方体との交点は\(A\)しかないので役に立たず、\(AB\)や\(AC\)を結んでもこの線分は立方体の面上にないので切断面にはなりません。(もちろん断面上には乗ってはいます)
そこで、\(BC\)上の点はすべて断面上にあることを利用することにして、思い切って\(BC\)を延長して立方体の面を拡張した面で考えることにします。直線\(BC\)と底面の辺の延長との交点を\(D,E\)とすれば、\(D,E\)は断面上にある点でかつ立方体の拡張させた面上にある点なので、\(AD\)、\(AE\)を結びます。\(AD,AE\)も断面上にあるので、辺との交点\(F,G\)も断面上にあり、\(AF,FB,AG,GC\)を結べば切断面の五角形を図示できます。

これらの図示方法の違いは、\(D,E\)が辺にあるか延長上にあるかの違いが原因です。

・立体の断面(曲面立体)
曲面で作られる立体の断面についてもまとめておきます。一部については細かい話は数ⅠAの範囲を超えるので知識としておさえる程度にしておきます。

①球

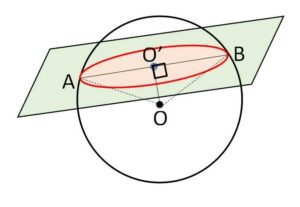
球を平面で切断すると切り方に関わらず、その断面は円になります。球をある平面に乗せてこの平面に垂直な平面で切ると円になるのは分かると思いますが、球は対称性のある立体なのでどのように平面で切っても回転させると同じ位置関係になるので、必ず断面は円です。
特に球の中心を通るような平面で切断すると断面である円の半径が最大となりこの円を大円とよび、それ以外の平面で切断したときの断面を小円とよびます。
また、球の中心\(O\)と断面である円の中心\(O’\)を結んだ\(OO’\)は断面に垂直になります。図の\(△OAB\)が二等辺三角形になることと\(O’\)が直径\(AB\)の中点であることから\(OO’ \perp AB\)であり、他の円の直径\(A’B’\)でも同じことが言えるので、任意の断面上の直線と\(OO’\)が垂直になるからです。

②円柱

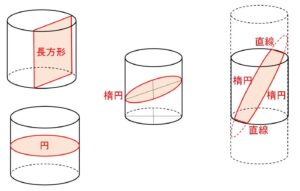
底面と上面に垂直な平面で切断すると、断面は長方形です。また底面と上面に平行な平面で切断すると、断面は円です。
切断する平面が傾いている場合は、底面と上面と交わらない場合には楕円(の全部)になります。これは平行面で切断した場合の断面の円と比べて、縦または横の一方向だけ拡大縮小されるからです。底面と上面と交わる場合は、円柱を上下に延長することで楕円の一部(楕円と直線からできる図形)であることが分かります。

③円錐

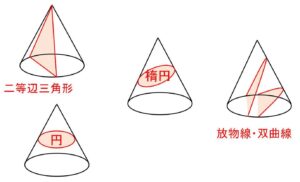
頂点を通るような平面で切断すると断面は母線を含むので二等辺三角形、底面に平行な平面で切断すると断面は円です。他にも色々な角度で切断すると、楕円・双曲線・放物線(まとめて二次曲線とよぶ)も現れます。

以上になります。お疲れ様です。
ここまで見て頂きありがとうございました。
next→三垂線の定理　back→空間図形の基本③(2平面)