三垂線の定理

三垂線の定理について見ていきます。

・三垂線の定理

平面\(α\)上の直線\(l\)、\(l\)上の点\(H\)、\(l\)上にない\(α\)上の点\(O\)、\(α\)上にない点\(P\)がある。このとき
(1)\(OP \perp α\)、\(OH \perp l\) ならば \(PH \perp l\)
(2)\(OP \perp α\)、\(PH \perp l\) ならば \(OH \perp l\)
(3)\(PH \perp l\)、\(OH \perp l\)、\(OP \perp OH\) ならば、\(OP \perp α\)

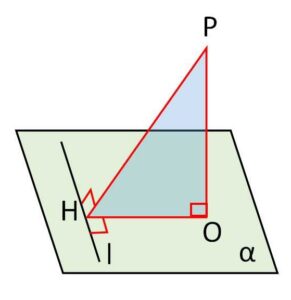
(解説)
3つの垂線\(OP,OH,PH\)が登場する定理です。直線同士の垂直、直線と平面の垂直が混じっていることに注意してください。(直線と平面の垂直は、平面上の任意の直線と垂直なので強いイメージ)
(1)(2)の結果は直線同士の垂直、(3)の結果は直線と平面の垂直です。
いずれも、直線と平面の垂直の定義「直線と平面上の任意の直線が垂直」と、直線と平面の垂直が言える定理「平面上の交わる2本の直線と垂直」(2本だけ調べればよい)がポイントです。

(証明)
いずれも平面\(OPH\)(平面\(β\)とする)と\(l\)の垂直を1クッションとして証明します。
(1)

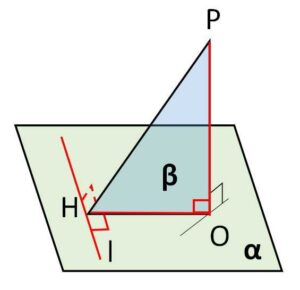
(\(β\)上の\(OH\)と\(l\)の垂直は条件より分かっているので、もう1本の垂直を調べます)
\(OP \perp α\) と、\(l\)が\(α\)上にあることから
\(OP \perp l\)・・・①
また仮定より
\(OH \perp l\)・・・②
\(OP,OH\)は\(β\)上にあるから①②より
\(β \perp l\)
よって、\(PH\)は\(β\)上にあるから
\(PH \perp l\)

(2)
((1)とほぼ同じです)

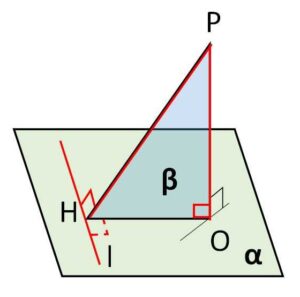
\(OP \perp α\) より
\(OP \perp l\)・・・③
また仮定より
\(PH \perp l\)・・・④
③④より
\(β \perp l\)
よって
\(OH \perp l\)

(3)

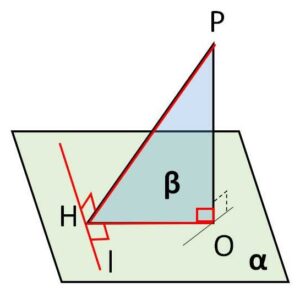
(\(OP\)と垂直な\(α\)上の2本の直線を探します。1つは条件より\(OH\)ですが、もう1つ\(l\)は同じく\(β\)との垂直から示します)
仮定 \(PH \perp l\)、\(OH \perp l\) より
\(β \perp l\)
よって \(OP \perp l\)・・・⑤
また仮定より \(OP \perp OH\)・・・⑥
したがって⑤⑥より
\(OP \perp α\)

以上になります。お疲れ様です。
ここまで見て頂きありがとうございました。
next→正多面体の種類　back→立体の断面