オイラーの多面体定理

オイラーの多面体定理です。

・オイラーの多面体定理

(解説)
正多面体に限らず、任意の凸多面体で成り立つ等式です。\(v,e,f\)は、\(vertex\)(頂点)、\(edge\)(辺)、\(face\)(面)の頭文字です(いずれも英語)。
3つのうち2つの個数が分かっていればもう1つを求めることができたり、\(v,e,f\)の数が合っているかの確認ができたりして便利な等式になっています。
結果だけ覚えておけばよいと思いますが、せっかくなので証明も軽くやっておきたいと思います。まず証明の準備から始めます。

(解説)

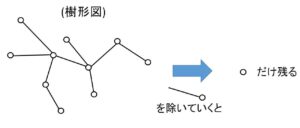
樹形図(面が無い)において、頂点と辺を1個ずつ1セットにして外側から外していくと、樹形図が途切れることなく短くなっていく。1個ずつ除くことから、辺と頂点の個数の差は変わることがなく、最終的に点だけが1個残る。よってもとの樹形図の頂点の個数は辺の個数より1つ多いので
\(V-E=1\)

続いて目的のオイラーの多面体定理の証明をします。

(オイラーの多面体定理の証明)

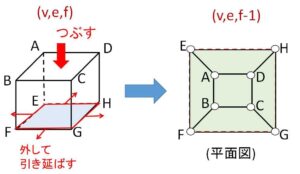
立体のままだと考えにくいので、底面を外して底面の枠が外周になるように引き延ばしながら立体を上からつぶします(上図)。

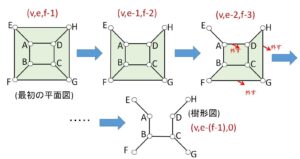
できた平面図から辺のみを1本ずつ面が1つ減るように抜いていくと、頂点の個数は変わらずに最終的に面がない樹形図になる。最初の平面図では、底を外したことで面の数が\(f-1\)個になっていることに注意すると、樹形図になるまで合計\(f-1\)回だけ辺を除いていることから、最終的に
「頂点\(v\)個、辺\(e-(f-1)\)個、(面\(0\)個)」
の樹形図になっている。すると等式 \(V-E=1\) より
\(v-\{e-(f-1)\}=1\)
整理して
\(v-e+f=2\)
を得る。

・オイラーの多面体定理と正多面体の種類
オイラーの多面体定理を用いて正多面体の種類がどうなるかを検討してみます。少し復習しておくと、正多面体の定義は次の通りです。

(1)各面は合同な正多角形
(2)各頂点に集まる面の数が等しい

面の形を正\(m\)角形 (\(m≧3\))、各頂点に集まる面の数(辺の数)を\(n\) (立体を作るには集まる面は3面以上必要なので\(n≧3\)) とします。最終的にはオイラーの多面体定理の等式を利用しますが、\(m,n,e,v,f\)の関係式をいくつか手に入れておきます。

正多面体の面をバラバラにしたときの合計の辺の数と頂点の数は、いずれも\(fm\)なので、
まず、辺の数\(e\)は1つの辺が2面で共有されていることから
\(\displaystyle\frac{fm}{2}=e\)
となるので
\(f=\displaystyle\frac{2e}{m}\)・・・①

次に、頂点の数\(v\)は1つの点が\(n\)個の面で共有されていることから
\(\displaystyle\frac{fm}{n}=v\)
①を代入して整理すると
\(v=\displaystyle\frac{2e}{n}\)・・・②

①②を \(v-e+f=2\) に代入して
\(\displaystyle\frac{2e}{n}-e+\displaystyle\frac{2e}{m}=2\)
(ここから先は整数問題です)
\((\displaystyle\frac{2}{n}-1+\displaystyle\frac{2}{m})e=2\)・・・③

\(mn\)倍して
\(-(mn-2m-2n)e=2mn\)
\(\{4-(m-2)(n-2)\}e=2mn\)
(\(m,n\)が大きすぎると左辺が負になるので範囲を絞れます)
\(m,n,e>0\) より
\(4-(m-2)(n-2)>0\)
\((m-2)(n-2)<4\)

\(m≧3,n≧3\) だから、左辺の組み合わせは次の5通りしかない。
\((m-2,n-2)=(1,1),(1,2),(2,1),(3,1),(1,3)\)
よって
\((m,n)=(3,3),(3,4),(4,3),(5,3),(3,5)\)・・・④
\(m=3,4,5\) だから正多面体の面は正三角形、正方形、正五角形のみであることが分かる。
④を③に代入して\(e\)を求めるとそれぞれ
\(e=6,12,12,30,30\)・・・⑤
④⑤を②①に代入すると、\(v,f\)はそれぞれ
\(v=4,6,8,20,12\)
\(f=4,8,6,12,20\)

\(f\)が面の数なので、正多面体は全部で「正四面体、正八面体、正六面体、正十二面体、正二十面体」の5種類になる。さらに辺の数などの各種情報も得られた。

(補足)
細かいことを言うと、得られた\(f=4,8,6,12,20\)は必要条件です。つまり正多面体として可能性があるのが5種類であって実際に正多面体として存在しているかどうか(組み立てることができるかどうか)は別途確認が必要になります。これは空間座標などを用いて調べることになります。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→正多面体と埋め込み　back→正多面体の種類