等面四面体についてです。
・等面四面体
4つの面が全て等しい鋭角三角形である四面体を等面四面体といいます。等面四面体は直方体の対角線を結んで作って考えるのが基本です(直方体への埋め込み)。
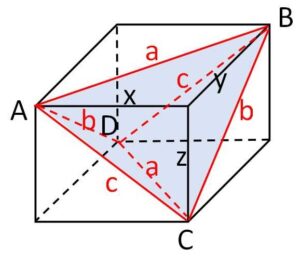
四面体の面の鋭角三角形の3辺の長さを\(a,b,c\)として、直方体の横・縦・高さの長さ\(x,y,z\)を求めてみます。三平方の定理より
\(x^2+y^2=a^2\)・・・①
\(y^2+z^2=b^2\)・・・②
\(z^2+x^2=c^2\)・・・③
①②③より\(x^2,y^2,z^2\)を求めると
\(x^2=\displaystyle\frac{1}{2}(a^2+c^2-b^2)\)・・・④
\(y^2=\displaystyle\frac{1}{2}(a^2+b^2-c^2)\)・・・⑤
\(z^2=\displaystyle\frac{1}{2}(b^2+c^2-a^2)\)・・・⑥
ここで\(△ABC\)は鋭角三角形だから
\(\cos A=\displaystyle\frac{a^2+c^2-b^2}{2ac}>0\)
よって \(a^2+c^2-b^2>0\)
同様に\(\angle B, \angle C\)について考えると
\(a^2+b^2-c^2>0\)、\(b^2+c^2-a^2>0\)
ゆえに④⑤⑥より\(x,y,z\)は正の数(実数)として存在し、それぞれ
\(x=\sqrt{\displaystyle\frac{1}{2}(a^2+c^2-b^2)}\)
\(y=\sqrt{\displaystyle\frac{1}{2}(a^2+b^2-c^2)}\)
\(z=\sqrt{\displaystyle\frac{1}{2}(b^2+c^2-a^2)}\)
等面四面体の体積を求めるにはこの\(x,y,z\)を利用して、直方体から削り出すことになります。また四面体の外接球と直方体の外接球は同じなので、外接球の半径\(R\)(直方体の対角線の半分)も求めることができます。
(例題)
四面体\(ABCD\)は、4つの面のどれも3辺の長さが\(7,8,9\)の三角形である。この四面体の体積と、外接球の半径の大きさ(4頂点を通る球の半径の大きさ)を求めよ。
(解答)
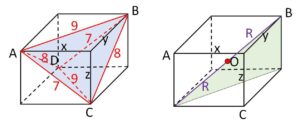
図のように直方体に四面体を埋め込む。三平方の定理より
\(x^2+y^2=81\)・・・①
\(y^2+z^2=64\)・・・②
\(z^2+x^2=49\)・・・③
(①+②+③)÷② より
\(x^2+y^2+z^2=97\)・・・④
④から②③①をそれぞれ引いて、正の平方根をとると
\(x=\sqrt{33}\)、\(y=4\sqrt{3}\)、\(z=4\)
よって四面体の体積\(V\)は、直方体から4つの三角錐を除くことにより
\(V=xyz-4\cdot\displaystyle\frac{1}{3}\cdot\displaystyle\frac{1}{2}xyz\)
\(=\displaystyle\frac{1}{3}xyz\)
\(=\displaystyle\frac{1}{3}\cdot\sqrt{33}\cdot4\sqrt{3}\cdot4\)
\(=16\sqrt{11}\)
また四面体の外接球と直方体の外接球は同じなので、球の半径\(R\)は直方体の対角線の半分になり
\(R=\displaystyle\frac{1}{2}\sqrt{x^2+y^2+z^2}\)
\(=\displaystyle\frac{1}{2}\sqrt{97}\) (④より)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→球の性質 back→正四面体と埋め込み