空間ベクトル(空間図形)の問題を解く際に、座標空間で考えるとよい場合があります。
その一例で複数のベクトルのなす角に関する例題について見ていきます。
(例題1)
図の直方体において、\(\overrightarrow{OA}=\vec{a}\), \(\overrightarrow{OB}=\vec{b}\), \(\overrightarrow{OC}=\vec{c}\), \(\overrightarrow{OP}=\vec{p}\) とする。\(\overrightarrow{OP}\)と\(\vec{a},\vec{b},\vec{c}\)のなす角をそれぞれ\(α,β,γ\)とするとき、次の等式が成り立つことを証明せよ。
\(\cos^2α+\cos^2β+\cos^2γ=1\)
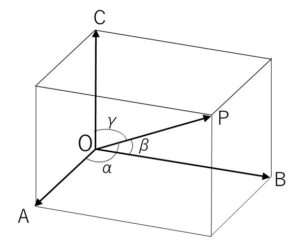
軸と\(\vec{p}\)のなす角が\(α,β,γ\)になり、それぞれの内積を求めていきますが、なす角について考えればよいので、軸方向のベクトルの大きさはどうでもよいので計算しやすい単位ベクトルを取り出します。
(解答)
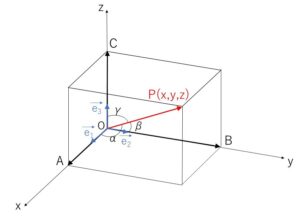
図のように座標空間を設定する。
\(\vec{e_1}=(1,0,0)\), \(\vec{e_2}=(0,1,0)\), \(\vec{e_3}=(0,0,1)\), \(\vec{p}=(x,y,z)\) とすると
\(\vec{p}\cdot\vec{e_1}=x=1\cdot|\vec{p}|\cosα\)
よって
\(\cosα=\displaystyle\frac{x}{|\vec{p}|}\)・・・①
同様に
\(\cosβ=\displaystyle\frac{y}{|\vec{p}|}\)・・・②
\(\cosα=\displaystyle\frac{z}{|\vec{p}|}\)・・・③
①②③より
\(\cos^2α+\cos^2β+\cos^2γ\)
\(=\displaystyle\frac{x^2+y^2+z^2}{|\vec{p}|^2}\)
\(=\displaystyle\frac{x^2+y^2+z^2}{x^2+y^2+z^2}\)
\(=1\)
よって証明された。
(別解)
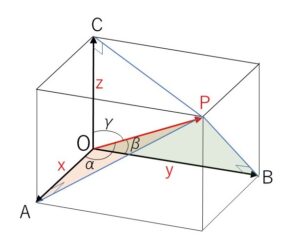
\(P\)から\(OA,OB,OC\)に垂線を下すと、垂線の足は\(A,B,C\)になる。
\(OA=x\), \(OB=y\), \(OC=z\) として
直角三角形\(POA\)について
\(\cosα=\displaystyle\frac{x}{OP}\)
同様に
\(\cosβ=\displaystyle\frac{y}{OP}\), \(\cosγ=\displaystyle\frac{z}{OP}\)
したがって
\(\cos^2α+\cos^2β+\cos^2γ\)
\(=\displaystyle\frac{x^2+y^2+z^2}{OP^2}\)
\(=\displaystyle\frac{x^2+y^2+z^2}{x^2+y^2+z^2}\)
\(=1\)
①②③から分かるように、\(\vec{p}\)の\(x,y,z\)成分(\(x,y,z\)方向の成分)は方向余弦によって決定されます。
(例題2)
\(\vec{a}=(1,0,0)\), \(\vec{b}=(\cos\displaystyle\frac{π}{3},\sin\displaystyle\frac{π}{3},0)\) とする。長さ\(1\)の空間ベクトル\(\vec{c}\)に対し \(\cosα=\vec{a}\cdot\vec{c}\), \(\cosβ=\vec{b}\cdot\vec{c}\) とおく。このとき次の不等式が成り立つことを示せ。
\(\cos^2α-\cosα\cosβ+\cos^2β≦\displaystyle\frac{3}{4}\)
\(\vec{a},\vec{b}\)は\(xy\)平面上の大きさ\(1\)のベクトルで、なす角が\(60°\)です。\(\vec{c}\)も大きさ\(1\)で(\(xy\)平面にあるとは限らない)、この2つのベクトルとなす角が\(α,β\)ということですが、この\(α,β\)は完全に自由に動くことができません。例えば\(α=β=0°\)は、\(\vec{c}\)の方向が\(\vec{a},\vec{b}\)と一致することなのであり得ません。よってある制約をもちながら\(α,β\)が動くことになり、その条件が証明する不等式になっています。ただ、空間でこの\(α,β\)の制約を図形的に考えるのは大変なので、問題で座標空間が設定されていることを踏まえて、ベクトルの成分で考えていくことになります。
(解答)
\(\vec{c}=(x,y,z)\)とおくと
\(x^2+y^2+z^2=1\)・・・①
また、\(\vec{a},\vec{b}\)との内積を考えて
\(\vec{c}\cdot\vec{a}=x=1\cdot1\cosα\)
\(\vec{c}\cdot\vec{b}=\displaystyle\frac{1}{2}x+\displaystyle\frac{\sqrt{3}}{2}y=1\cdot1\cosβ\)
よって
\(x=\cosα\)・・・②
\(\displaystyle\frac{1}{2}x+\displaystyle\frac{\sqrt{3}}{2}y=\cosβ\)・・・③
②を③に代入して
\(\displaystyle\frac{1}{2}\cosα+\displaystyle\frac{\sqrt{3}}{2}y=\cosβ\)
\(y=\displaystyle\frac{1}{\sqrt{3}}(2\cosβ-\cosα)\)・・・③’
②,③’ を①に代入して
\(\cos^2α+\displaystyle\frac{1}{3}(2\cosβ-\cosα)^2+z^2=1\)
\(z^2=1-\displaystyle\frac{4}{3}(\cos^2α-\cosα\cosβ+\cos^2β)\)・・・①’
実数\(z\)が存在するためには
\(1-\displaystyle\frac{4}{3}(\cos^2α-\cosα\cosβ+\cos^2β)≧0\)
(このとき②③’より\(x,y\)も実数となる)
したがって
\(\cos^2α-\cosα\cosβ+\cos^2β≦\displaystyle\frac{3}{4}\)
このとき、②③’より \(x=1\), \(y=\displaystyle\frac{1}{\sqrt{3}}\)
①’より \(z^2=-\displaystyle\frac{1}{3}\) だから、\(z=±\displaystyle\frac{1}{\sqrt{3}}i\) と虚数になってしまい、座標空間にベクトルを設定することができません。そしてもちろん証明した不等式の左辺は、\(1-1+1=1\) となり、不等式は満たされません。
(別解)
\(x^2+y^2+z^2=1\)・・・①
\(x=\cosα\)・・・②
\(\displaystyle\frac{1}{2}x+\displaystyle\frac{\sqrt{3}}{2}y=\cosβ\)・・・③
を導くことまでは同じ。
\(\cos^2α-\cosα\cosβ+\cos^2β\)
\(=x^2-x(\displaystyle\frac{1}{2}x+\displaystyle\frac{\sqrt{3}}{2}y)+(\displaystyle\frac{1}{2}x+\displaystyle\frac{\sqrt{3}}{2}y)^2\)
\(=\displaystyle\frac{3}{4}(x^2+y^2)\)
\(=\displaystyle\frac{3}{4}(1-z^2)≦\displaystyle\frac{3}{4}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→空間の位置ベクトルと分点・重心 back→折れ線の長さ