空間の位置ベクトルと分点・重心

空間の位置ベクトル、分点や重心のベクトルについて見ていきます。
平面ベクトルの場合と内容はほぼ同じです。

・空間の位置ベクトル

・位置ベクトル

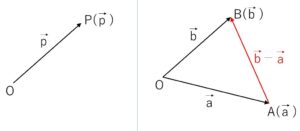
空間上で定点\(O\)をとると、空間上の任意の点の位置は\(O\)を基準(始点)としたベクトルを用いて表すことできます。つまり空間上の点\(P\)の位置は

\(\overrightarrow{OP}=\vec{p}\)

によって定まることになります。このとき\(\vec{p}\)を\(O\)を基準とする点\(P\)の位置ベクトルといい、位置ベクトルが\(\vec{p}\)である点\(P\)を \(P(\vec{p})\) と表します。

基準となる点\(O\)のとりかたに決まりはありませんが、特に\(O\)を座標空間上の原点にとると、\(\vec{p}\)の成分と点\(P\)の座標が一致するので、原点を基準とすることが多いです。

また、2点 \(A(\vec{a})\), \(B(\vec{b})\) について

\(\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=\vec{b}-\vec{a}\)

となるので、\(\overrightarrow{AB}\) は終点\(B\)の位置ベクトルから始点\(A\)の位置ベクトルを引いた差で表されることになります。

・分点・重心の位置ベクトル
3点\(A(\vec{a})\), \(B(\vec{b})\), \(C(\vec{c})\) について

(1)線分\(AB\)を\(m:n\)の比に内分する点\(P(\vec{p})\)の位置ベクトルは
\(\vec{p}=\displaystyle\frac{n\vec{a}+m\vec{b}}{m+n}\)

とくに線分\(AB\)の中点\(M(\vec{m})\)の位置ベクトルは
\(\vec{m}=\displaystyle\frac{\vec{a}+\vec{b}}{2}\)

(2)線分\(AB\)を\(m:n\)の比に外分する点\(Q(\vec{q})\)の位置ベクトルは
\(\vec{q}=\displaystyle\frac{-n\vec{a}+m\vec{b}}{m-n}\)

(3)三角形\(ABC\)の重心\(G(\vec{g})\)の位置ベクトルは
\(\vec{g}=\displaystyle\frac{\vec{a}+\vec{b}+\vec{c}}{3}\)

(解説)
(1)内分点について

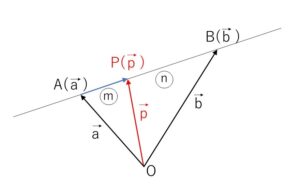
図より
\(\vec{p}=\vec{a}+\displaystyle\frac{m}{m+n}(\vec{b}-\vec{a})\)

\(=\displaystyle\frac{n\vec{a}+m\vec{b}}{m+n}\)

とくに \(m=n\) とすれば中点となり
\(\vec{m}=\displaystyle\frac{\vec{a}+\vec{b}}{2}\)

(2)外分点について

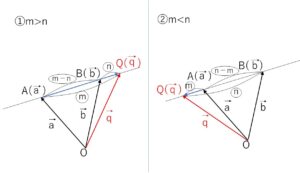
①\(m>n\)のとき
\(\vec{q}=\vec{a}+\displaystyle\frac{m}{m-n}(\vec{b}-\vec{a})\)

\(=\displaystyle\frac{-n\vec{a}+m\vec{b}}{m-n}\)

②\(m<n\)のとき
\(\vec{q}=\vec{a}+\displaystyle\frac{m}{n-m}(\vec{a}-\vec{b})\)

\(=\vec{a}+\displaystyle\frac{m}{m-n}(\vec{b}-\vec{a})\)

\(=\displaystyle\frac{-n\vec{a}+m\vec{b}}{m-n}\)

(3)重心について

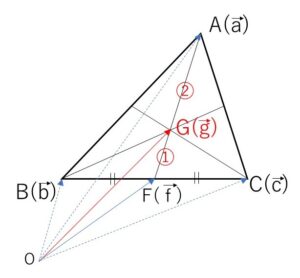
線分\(BC\)の中点を\(F(\vec{f})\)とすると
\(\vec{f}=\displaystyle\frac{\vec{b}+\vec{c}}{2}\)

\(G\)は線分\(AF\)を\(2:1\)の比に内分する点だから
\(\vec{g}=\displaystyle\frac{\vec{a}+2\vec{f}}{2+1}\)

\(=\displaystyle\frac{\vec{a}+\vec{b}+\vec{c}}{3}\)

・分点・重心の位置ベクトル(成分表示)
上記の分点・重心の位置ベクトルの公式を成分表示にすることにより、分点・重心の座標を求めることができます。

3点 \(A(x_1,y_1,z_1)\), \(B(x_2,y_2,z_2)\), \(C(x_3,y_3,z_3)\) について

(1)線分\(AB\)を\(m:n\)の比に内分する点\(P\)の座標は
\((\displaystyle\frac{nx_1+mx_2}{m+n},\displaystyle\frac{ny_1+my_2}{m+n},\displaystyle\frac{nz_1+mz_2}{m+n})\)

とくに線分\(AB\)の中点\(M\)の座標は
\((\displaystyle\frac{x_1+x_2}{2},\displaystyle\frac{y_1+y_2}{2},\displaystyle\frac{z_1+z_2}{2})\)

(2)線分\(AB\)を\(m:n\)の比に外分する点\(Q\)の座標は
\((\displaystyle\frac{-nx_1+mx_2}{m-n},\displaystyle\frac{-ny_1+my_2}{m-n},\displaystyle\frac{-nz_1+mz_2}{m-n})\)

(3)三角形\(ABC\)の重心\(G\)の座標は
\((\displaystyle\frac{x_1+x_2+x_3}{3},\displaystyle\frac{y_1+y_2+y_3}{3},\displaystyle\frac{z_1+z_2+z_3}{3})\)

(解説)
(1)内分点の座標について
原点を位置ベクトルの基準とする。\(P(x,y,z)\)とおくと、\(\vec{p}=\displaystyle\frac{n\vec{a}+m\vec{b}}{m+n}\) より

\((x,y,z)=\displaystyle\frac{n}{m+n}(x_1,y_1,z_1)+\displaystyle\frac{m}{m+n}(x_2,y_2,z_2)\)

よって
\((x,y,z)=(\displaystyle\frac{nx_1+mx_2}{m+n},\displaystyle\frac{ny_1+my_2}{m+n},\displaystyle\frac{nz_1+mz_2}{m+n})\)

中点、(2)外分点、(3)重心についても同様に示せます。

(例題)
四面体\(ABCD\)において、頂点\(A\)と\(△BCD\)の重心\(E\)とを結ぶ線分\(AE\)を\(3:1\)の比に内分する点を\(G\)とする。このとき、次の等式が成り立つことを示せ。
\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\vec{0}\)

(解答)

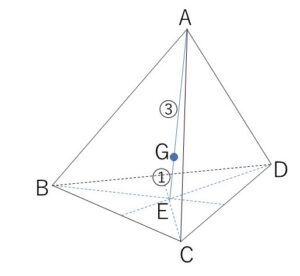
\(A(\vec{a})\), \(B(\vec{b})\), \(C(\vec{c})\), \(D(\vec{d})\) とおく。

\(E(\vec{e})\) について
\(\vec{e}=\displaystyle\frac{\vec{b}+\vec{c}+\vec{d}}{3}\)

\(G(\vec{g})\) について
\(\vec{g}=\displaystyle\frac{\vec{a}+3\vec{e}}{3+1}=\displaystyle\frac{\vec{a}+\vec{b}+\vec{c}+\vec{d}}{4}\)

よって
\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}\)

\(=(\vec{a}-\vec{g})+(\vec{b}-\vec{g})+(\vec{c}-\vec{g})+(\vec{d}-\vec{g})\)

\(=\vec{a}+\vec{b}+\vec{c}+\vec{d}-4\vec{g}\)

\(=\vec{0}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→点Pの位置ベクトルと体積比の基礎　back→複数のベクトルのなす角