同一直線上にある条件

空間における点が同一直線上にある条件について見ていきます。

・同一直線上にある条件

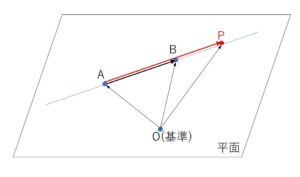
異なる2点を\(A(\vec{a}),B(\vec{b})\)とすると、次のことが成り立ちます。

点\(P(\vec{p})\)が直線\(AB\)上にある

\(⇔\)　\(\overrightarrow{AP}=k\overrightarrow{AB}\)　(\(k\)は実数)

\(⇔\)　\(\vec{p}=(1-k)\vec{a}+k\vec{b}\)

\(⇔\)　\(\vec{p}=s\vec{a}+t\vec{b}\) かつ \(s+t=1\)　(\(s,t\)は実数)

(解説)
\(P\)が直線\(AB\)上にあるとき
\(\overrightarrow{AP}/\!/\overrightarrow{AB}\) または \(\overrightarrow{AP}=\vec{0}\) より、\(k\)を実数とすれば

\(\overrightarrow{AP}=k\overrightarrow{AB}\)

よって
\(\vec{p}-\vec{a}=k(\vec{b}-\vec{a})\)
整理すると
\(\vec{p}=(1-k)\vec{a}+k\vec{b}\)

さらに右辺の係数の和が \((1-k)+k=1\) となることに着目して
\(1-k=s\),　\(k=t\) とおくと、\(s,t\)は実数で

\(\vec{p}=s\vec{a}+t\vec{b}\) かつ \(s+t=1\)

(例題1)
四面体\(ABCD\)の辺\(AB,CD,AC,BD\)の中点を、それぞれ\(K,L,M,N\)とし、更に\(KL\)の中点を\(P\)とすると、\(M,N,P\)は同一直線上にあることを証明せよ。

(解答)

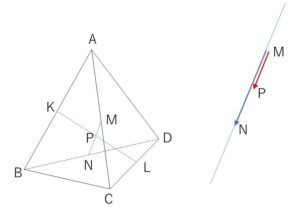
\(A(\vec{a})\), \(B(\vec{b})\), \(C(\vec{c})\), \(D(\vec{d})\) とおく。

\(K(\vec{k})\), \(L(\vec{l})\), \(M(\vec{m})\), \(N(\vec{n})\) の位置ベクトルはそれぞれ

\(\vec{k}=\displaystyle\frac{\vec{a}+\vec{b}}{2}\),　\(\vec{l}=\displaystyle\frac{\vec{c}+\vec{d}}{2}\),　\(\vec{m}=\displaystyle\frac{\vec{a}+\vec{c}}{2}\),　\(\vec{n}=\displaystyle\frac{\vec{b}+\vec{d}}{2}\)

また、\(P(\vec{p})\) の位置ベクトルは
\(\vec{p}=\displaystyle\frac{\vec{k}+\vec{l}}{2}=\displaystyle\frac{\vec{a}+\vec{b}+\vec{c}+\vec{d}}{4}\)

よって
\(\overrightarrow{MN}=\vec{n}-\vec{m}=\displaystyle\frac{\vec{b}+\vec{d}-\vec{a}-\vec{c}}{2}\)

\(\overrightarrow{MP}=\vec{p}-\vec{m}=\displaystyle\frac{\vec{b}+\vec{d}-\vec{a}-\vec{c}}{4}\)

したがって
\(\overrightarrow{MN}=2\overrightarrow{MP}\) であるから
\(M,N,P\)は同一直線上にある。

(例題2)
\(O,A,B,C\)は同一平面上にない4点とし、線分\(OA,BC\)の中点をそれぞれ\(M,N\)、\(R\)を \(\overrightarrow{OR}=α\overrightarrow{OA}+β\overrightarrow{OB}+γ\overrightarrow{OC}\) (\(α,β,γ\)は実数) を満たす点とする。\(R\)が直線\(MN\)上の点であるための条件は、\(α+β=\displaystyle\frac{1}{2}\),　\(β=γ\) であることを示せ。

(解答)
\(R\)が\(MN\)上にあるので、\(k\)を実数として
\(\overrightarrow{OR}=(1-k)\overrightarrow{OM}+k\overrightarrow{ON}\)
\(=(1-k)\cdot\displaystyle\frac{1}{2}\overrightarrow{OA}+k\cdot\displaystyle\frac{\overrightarrow{OB}+\overrightarrow{OC}}{2}\)

\(=\displaystyle\frac{1-k}{2}\overrightarrow{OA}+\displaystyle\frac{k}{2}\overrightarrow{OB}+\displaystyle\frac{k}{2}\overrightarrow{OC}\)・・・①

\(O,A,B,C\)が同一平面上にないので、\(\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}\)は1次独立。

\(\overrightarrow{OR}=α\overrightarrow{OA}+β\overrightarrow{OB}+γ\overrightarrow{OC}\)・・・②

①②の右辺の係数を比較して
\(\displaystyle\frac{1-k}{2}=α\)・・・③
\(\displaystyle\frac{k}{2}=β\)・・・④
\(\displaystyle\frac{k}{2}=γ\)・・・⑤

③④⑤を満たす実数\(k\)が存在すればよいから、
④⑤より
\(β=γ\)・・・(i)

③④より
\(\displaystyle\frac{1}{2}-β=α\)
\(α+β=\displaystyle\frac{1}{2}\)・・・(ii)

(逆に(i),(ii)を満たすとき、③④⑤を満たす実数\(k\)が存在する)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→交点のベクトル、点の一致　back→点Pの位置ベクトルと体積比の基礎