点\(P\)が平面\(ABC\)上にある条件について見ていきます。
・同一平面上にある条件
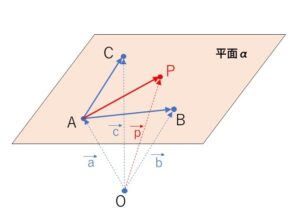
同じ直線上にない3点 \(A(\vec{a})\), \(B(\vec{b})\), \(C(\vec{c})\) を通る平面を\(α\)とします。(\(A,B,C\)が同一直線上にあると平面が1つに定まらない)
点\(P(\vec{p})\)が\(α\)上にあるとき、実数\(s,t\)を用いて\(\overrightarrow{AP}\)を次のように表すことができます。
\(\overrightarrow{AP}=s\overrightarrow{AB}+t\overrightarrow{AC}\)・・・①
(\(A,B,C\)が一直線上にないためにこの形で表せます。)
よって
\(\vec{p}-\vec{a}=s(\vec{b}-\vec{a})+t(\vec{c}-\vec{a})\)
\(\vec{p}=(1-s-t)\vec{a}+s\vec{b}+t\vec{c}\)
ここで、係数の和が \((1-s-t)+s+t=1\) になることに着目して
\(1-s-t=r\) とおくと\(r\)も実数であり
\(\vec{p}=r\vec{a}+s\vec{b}+t\vec{c}\) (\(r+s+t=1\))・・・②
となります。逆に②のとき下から上に辿ることによって①となるので、②が成り立つとき\(P\)が平面\(α\)上に存在することになります。
また、②のベクトルの等式について位置ベクトルの基準を\(O\)とすると次のように表されます。
\(\overrightarrow{OP}=r\overrightarrow{OA}+s\overrightarrow{OB}+t\overrightarrow{OC}\) (\(r+s+t=1\))
\(A(\vec{a}),B(\vec{b}),C(\vec{c})\) を同一直線上にない3点とするとき、\(r,s,t\)を実数として
点\(P(\vec{p})\)が平面\(ABC\)上にある
\(⇔\) \(\overrightarrow{AP}=s\overrightarrow{AB}+t\overrightarrow{AC}\)
\(⇔\) \(\vec{p}=r\vec{a}+s\vec{b}+t\vec{c}\) (\(r+s+t=1\))
・三角形\(ABC\)の周及び内部にある条件
平面\(ABC\)上に点\(P\)がある条件は上記の通りですが、この\(r,s,t\)に制約を加えることで三角形\(ABC\)の周及び内部に関する条件を表すことができます。
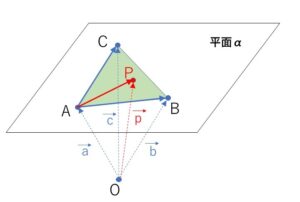
\(\overrightarrow{AP}=s\overrightarrow{AB}+t\overrightarrow{AC}\)・・・①
について、点\(P\)が三角形\(ABC\)の周及び内部にある条件は次の通りでした。
\(0≦s+t≦1\), \(s≧0\), \(t≧0\)
ここで、\(s≧0\), \(t≧0\) のとき、\(0≦s+t\) は保証されるので次のように条件を置き換えてもよいことになります。
\(s+t≦1\), \(s≧0\), \(t≧0\)
①を変形した式が
\(\vec{p}=r\vec{a}+s\vec{b}+t\vec{c}\) (\(r+s+t=1\))・・・②
であり、\(s+t=1-r\) なので、\(s+t≦1\) を \(1-r≦1\) と置き換えると
\(r≧0\)
したがって三角形\(ABC\)の周及び内部に点\(P\)がある条件は次の通りです。
\(\vec{p}=r\vec{a}+s\vec{b}+t\vec{c}\) (\(r+s+t=1\))
\(r≧0\), \(s≧0\), \(t≧0\)
(例題)
4点 \(A(3,2,0)\), \(B(3,1,3)\), \(C(1,4,-3)\), \(P(1,y,0)\) が同一平面上にあるような実数\(y\)の値を求めよ。
②\(\vec{p}=r\vec{a}+s\vec{b}+t\vec{c}\) (\(r+s+t=1\))
のどちからで解くことになります。②は①を変形して\(\vec{a}\)の係数の文字を置き換えただけなので、本質的には同じです。
(解答①)
\(A(3,2,0)\), \(B(3,1,3)\), \(C(1,4,-3)\), \(P(1,y,0)\) より
\(\overrightarrow{AP}=(-2,y-2,0)\)
\(\overrightarrow{AB}=(0,-1,3)\)
\(\overrightarrow{AC}=(-2,2,-3)\)
\(P\)が平面\(ABC\)上にあり、\(\overrightarrow{AB},\overrightarrow{AC}\) は平行でないから(\(A,B,C\)が同一直線上にないということ)
\(\overrightarrow{AP}=s\overrightarrow{AB}+t\overrightarrow{AC}\) (\(s,t\)は実数)
とおける。
\((-2,y-2,0)=s(0,-1,3)+t(-2,2,-3)\)\(=(-2t,-s+2t,3s-3t)\)
係数を比較して
\(-2=-2t\)・・・(i)
\(y-2=-s+2t\)・・・(ii)
\(0=3s-3t\)・・・(iii)
(i)より \(t=1\)
これと(iii)より \(s=1\)
よって(ii)より
\(y=3\)
(解法②)
\(A(3,2,0)\), \(B(3,1,3)\), \(C(1,4,-3)\), \(P(1,y,0)\) より
\(\overrightarrow{AB}=(0,-1,3)\)
\(\overrightarrow{AC}=(-2,2,-3)\)
\(\overrightarrow{AB},\overrightarrow{AC}\) は平行でないから、\(A,B,C\)は同一直線上にない。よって、\(A(\vec{a})\), \(B(\vec{b})\), \(C(\vec{c})\), \(P(\vec{p})\) とおくと
\(\vec{p}=r\vec{a}+s\vec{b}+t\vec{c}\) (\(r+s+t=1\))
と表せる。よって
\((1,y,0)=(3r+3s+t,2r+s+4t,3s-3t)\) かつ \(r+s+t=1\)
係数を比較して
\(1=3r+3s+t\)・・・(1)
\(y=2r+s+4t\)・・・(2)
\(0=3s-3t\)・・・(3)
かつ \(r+s+t=1\)・・・(4)
(1)(4)より
\(1=3(1-t)+t\)
よって \(t=1\)
(3)より \(s=1\)
(4)より \(r=-1\)
したがって(2)より
\(y=3\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→同一平面上にある条件② back→交点のベクトル・点の一致