同一平面上の条件に関する例題です。
(例題1)
四面体\(OABC\)において、\(\overrightarrow{OA}=\vec{a}\), \(\overrightarrow{OB}=\vec{b}\), \(\overrightarrow{OC}\) とする。線分\(OA\)を\(2:1\)に内分する点を\(P\)、線分\(PB\)を\(2:1\)に内分する点を\(Q\)、線分\(QC\)を\(2:1\)に内分する点を\(R\)、直線\(OR\)と三角形\(ABC\)との交点を\(S\)とする。
(1)\(\overrightarrow{OR}\)を\(\vec{a},\vec{b},\vec{c}\)を用いて表せ。
(2)\(\overrightarrow{OS}\)を\(\vec{a},\vec{b},\vec{c}\)を用いて表せ。
(3)四面体\(OABC\)の体積を\(V_1\)、四面体\(OPQR\)の体積を\(V_2\)とするとき、\(\displaystyle\frac{V_2}{V_1}\) を求めよ。
(解答)
(1)
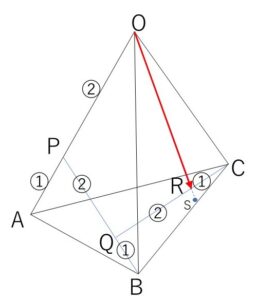
\(\overrightarrow{OP}=\vec{p}\)、\(\overrightarrow{OQ}=\vec{q}\)、\(\overrightarrow{OR}=\vec{r}\) とおくと
\(\vec{r}=\displaystyle\frac{\vec{q}+2\vec{c}}{3}\)
\(=\displaystyle\frac{1}{3}\cdot\displaystyle\frac{\vec{p}+2\vec{b}}{3}+\displaystyle\frac{2}{3}\vec{c}\)
\(=\displaystyle\frac{1}{9}\cdot\displaystyle\frac{2}{3}\vec{a}+\displaystyle\frac{2}{9}\vec{b}+\displaystyle\frac{2}{3}\vec{c}\)
\(=\displaystyle\frac{2}{27}\vec{a}+\displaystyle\frac{2}{9}\vec{b}+\displaystyle\frac{2}{3}\vec{c}\)
(2)
\(\overrightarrow{OS}=k\overrightarrow{OR}\)
\(=\displaystyle\frac{2}{27}k\vec{a}+\displaystyle\frac{2}{9}k\vec{b}+\displaystyle\frac{2}{3}k\vec{c}\)
ここで、\(A,B,C\)は三角形を成しているので同一直線上にないことと、\(R\)が四面体の内部にあるため\(S\)は三角形\(ABC\)の内部にあることから、平面\(ABC\)上に\(S\)がある条件を考えて
\(\displaystyle\frac{2}{27}k+\displaystyle\frac{2}{9}k+\displaystyle\frac{2}{3}k=1\)
よって \(k=\displaystyle\frac{27}{26}\)
したがって
\(\overrightarrow{OS}\)
\(=\displaystyle\frac{27}{26}(\displaystyle\frac{2}{27}\vec{a}+\displaystyle\frac{2}{9}\vec{b}+\displaystyle\frac{2}{3}\vec{c})\)
\(=\displaystyle\frac{1}{13}\vec{a}+\displaystyle\frac{3}{13}\vec{b}+\displaystyle\frac{9}{13}\vec{c}\)
(3)
①高さが同じのとき (体積比)=(底面積の比)
②底面積が同じのとき (体積比)=(高さの比)
です。高さの比を考えるときは、底面に垂線を下すことになります。問題文で3つの比が登場しているので3回に分けて比をとっていきます。
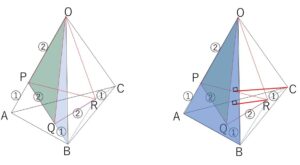
四面体\(OPQR\)と四面体\(OPBR\)は、底面を平面\(OAB\)上にある面とすると、高さが共通なので底面積の比を考えると
\(V_2=\displaystyle\frac{2}{3}(四面体OPBR)\)・・・(i)
同様に、四面体\(OPBR\)と四面体\(OABR\)について
\((四面体OPBR)=\displaystyle\frac{2}{3}(四面体OABR)\)・・・(ii)
また、四面体\(OABR\)と四面体\(OABC\)は、底面を\(OAB\)とすると共通で、\(QR:QC=2:3\) より、\((四面体OABRの高さ):(四面体OABCの高さ)=2:3\) となるので
\((四面体OABR)=\displaystyle\frac{2}{3}V_1\)・・・(iii)
(i)(ii)(iii)より
\(V_2=\displaystyle\frac{2^3}{3^3}V_1\)
したがって
\(\displaystyle\frac{V_2}{V_1}=\displaystyle\frac{8}{27}\)
(例題2)
図のような1辺の長さ\(1\)の立方体\(OABC-DEFG\)を考える。辺\(AE\)の中点を\(M\)、辺\(DG\)の中点を\(N\)とする。\(X\)を辺\(DE\)上の点、\(Y\)を辺\(BC\)上の点とし、\(DX\)の長さを\(x\)、\(CY\)の長さを\(y\)とする。このとき4点\(X,M,Y,N\)が同一平面上にあるための必要十分条件を\(x\)と\(y\)を用いて表せ。
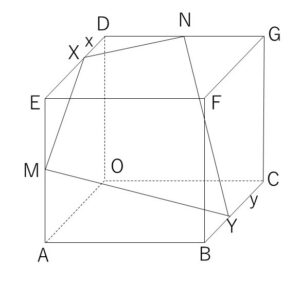
①\(\overrightarrow{XY}=s\overrightarrow{XM}+t\overrightarrow{XN}\)
②\(\overrightarrow{OY}=r\overrightarrow{OX}+s\overrightarrow{OM}+t\overrightarrow{ON}\) (\(r+s+t=1\))
のどちらかを利用しますが、解答では②を使いたいと思います。
また、\(Y\)が\(BC\)上にあることももちろん使います。
(解答)
\(\overrightarrow{OA}=\vec{a}\), \(\overrightarrow{OC}=\vec{c}\), \(\overrightarrow{OD}=\vec{d}\) とおく。
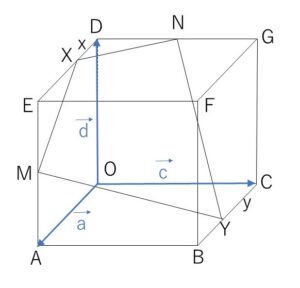
立方体は1辺の長さが\(1\)だから
\(\overrightarrow{OX}=\vec{d}+x\vec{a}\)
\(\overrightarrow{OM}=\vec{a}+\displaystyle\frac{1}{2}\vec{d}\)
\(\overrightarrow{ON}=\vec{d}+\displaystyle\frac{1}{2}\vec{c}\)
また
\(\overrightarrow{OY}=\vec{c}+y\vec{a}\)\(=y\vec{a}+\vec{c}\)・・・(i)
ここで、\(X,M,N\)は一直線上にないので、平面\(XMN\)上に点\(Y\)がある必要十分条件は
\(\overrightarrow{OY}=r\overrightarrow{OX}+s\overrightarrow{OM}+t\overrightarrow{ON}\)・・・(ii) (\(r+s+t=1\))
となる実数\(r,s,t\)が存在することである。
((ii)の右辺)
\(=r(x\vec{a}+\vec{d})+s(\vec{a}+\displaystyle\frac{1}{2}\vec{d})+t(\displaystyle\frac{1}{2}\vec{c}+\vec{d})\)
\(=(rx+s)\vec{a}+\displaystyle\frac{1}{2}t\vec{c}+(r+\displaystyle\frac{1}{2}s+t)\vec{d}\)・・・(iii)
\(\vec{a},\vec{b},\vec{c}\) は同一平面上にはないので(i)(iii)の係数を比較して
\(y=rx+s\)・・・(I)
\(1=\displaystyle\frac{1}{2}t\)・・・(II)
\(0=r+\displaystyle\frac{1}{2}s+t\)・・・(III)
かつ \(r+s+t=1\)・・・(IV)
(II)より \(t=2\)
(III),(IV) より
\(s=2\), \(r=-3\)
したがって(I)より
\(y=-3x+2\)
が成り立てば、(ii)を満たす実数\(r,s,t\)が存在することになる。
答 \(y=-3x+2\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→直線の方程式 back→同一平面上にある条件①