格子点の個数と極限に関する例題です。
(例題1)
2つの放物線 \(y=x^2\), \(y=(x-n)^2+n^2\) (\(n\)は自然数) と\(y\)軸で囲まれた部分(境界線を含む)にあって、\(x\)座標、\(y\)座標がともに整数である点の個数を\(a_n\)とする。
(1)\(a_n\)を求めよ。
(2)\(\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n^4}(a_1+a_2+\cdots+a_n)\) を求めよ。
(解答)
(1)
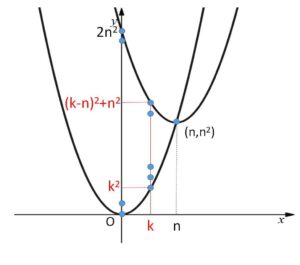
\(x,y\)座標ともに整数である点を格子点と名付ける。
\(x=k\) 上の格子点は、\(y\)座標を列挙すると
\(y=k^2,k^2+1,\cdots,(k-n)^2+n^2\)
となるから、その個数は
\((k-n)^2+n^2-k^2\color{red}{+1}\)\(=-2nk+2n^2+1\)
よって
\(a_n=\displaystyle\sum_{k=0}^{n}(-2nk+2n^2+1)\)
\(=-2n\displaystyle\sum_{k=0}^{n}k+(2n^2+1)\displaystyle\sum_{k=0}^{n}1\)
\(=-2n\cdot\displaystyle\frac{1}{2}n(n+1)+(2n^2+1)(n+1)\)
\(=n^3+n^2+n+1\)
(2)
シグマ公式は展開せずに、そのまま極限を求めたほうが楽です。
\(\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n^4}(a_1+a_2+\cdots+a_n)\)
\(=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n^4}\displaystyle\sum_{k=1}^{n}(k^3+k^2+k+1)\)
\(=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n^4}\left\{\displaystyle\frac{1}{4}n^2(n+1)^2+\displaystyle\frac{1}{6}n(n+1)(2n+1)+\displaystyle\frac{1}{2}n(n+1)+n\right\}\)
(\(n^4\)で割るのでほとんど項が\(0\)に収束します)
\(=\displaystyle\lim_{n \to \infty}\left\{\displaystyle\frac{1}{4}(1+\displaystyle\frac{1}{n})^2+\displaystyle\frac{1}{6n}(1+\displaystyle\frac{1}{n})(2+\displaystyle\frac{1}{n})+\displaystyle\frac{1}{2n^2}(1+\displaystyle\frac{1}{n})+\displaystyle\frac{1}{n^3}\right\}\)
\(=\displaystyle\frac{1}{4}\)
(例題2)
\(a,m\)は自然数で\(a\)は定数とする。\(xy\)平面上の点\((a,m)\)を頂点とし、原点と点\((2a,0)\)を通る放物線を考える。この放物線と\(x\)軸で囲まれる領域の面積を\(S_m\)、この領域の内部および境界線上にある格子点の数を\(L_m\)とする。ただし\(xy\)平面上の格子点とはその点の\(x\)座標と\(y\)座標がともに整数となる点のことである。
(1)\(S_m\)を求めよ。
(2)\(\displaystyle\lim_{m \to \infty}\displaystyle\frac{L_m}{S_m}\) を求めよ。
(解答)
(1)
放物線は \(y=k(x-a)^2+m\) とおけて、これが原点を通るから
\(0=ka^2+m\)
よって \(k=-\displaystyle\frac{m}{a^2}\)
ゆえに放物線は
\(y=-\displaystyle\frac{m}{a^2}(x-a)^2+m\)
\(=-\displaystyle\frac{m}{a^2}x(x-2a)\) (問題文の設定からも分かる)
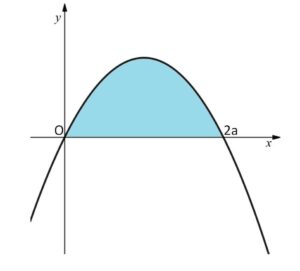
したがって
\(S_{m}=\displaystyle\int_{0}^{2a}\left\{-\displaystyle\frac{m}{a^2}x(x-2a)\right\}dx\)
\(=-\displaystyle\frac{1}{6}(-\displaystyle\frac{m}{a^2})(2a-0)^3\)
\(=\displaystyle\frac{4am}{3}\)
(2)
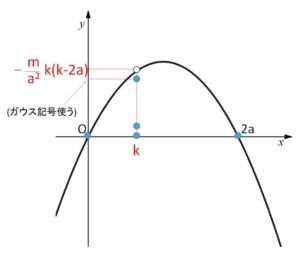
\([x]\)を\(x\)を超えない最大の整数とする。
領域内において、\(x=k\) 上の格子点の個数は
\(\left[-\displaystyle\frac{m}{a^2}k(k-2a)\right]-0+1=\)\(\left[-\displaystyle\frac{m}{a^2}k(k-2a)\right]+1\)
また、\(x-1<[x]≦x\) より
\(-\displaystyle\frac{m}{a^2}k(k-2a)-1<\left[-\displaystyle\frac{m}{a^2}k(k-2a)\right]≦-\displaystyle\frac{m}{a^2}k(k-2a)\)
よって、辺々\(1\)を加えて
\(-\displaystyle\frac{m}{a^2}k(k-2a)<\left[-\displaystyle\frac{m}{a^2}k(k-2a)\right]+1≦-\displaystyle\frac{m}{a^2}k(k-2a)+1\)・・・①
\(L_m=\displaystyle\sum_{k=0}^{2a}\{\left[-\displaystyle\frac{m}{a^2}k(k-2a)\right]+1\}\)
だから、①で\(k=0~2a\) の和をとると
\(\displaystyle\sum_{k=0}^{2a}\left\{-\displaystyle\frac{m}{a^2}k(k-2a)\right\}<L_m≦\displaystyle\sum_{k=0}^{2a}\left\{-\displaystyle\frac{m}{a^2}k(k-2a)+1\right\}\)
ここで
\(\displaystyle\sum_{k=0}^{2a}\left\{-\displaystyle\frac{m}{a^2}k(k-2a)\right\}\)
\(=\displaystyle\sum_{k=0}^{2a}\left\{-\displaystyle\frac{m}{a^2}k^2+\displaystyle\frac{2m}{a}k\right\}\)
(\(k=1\)スタートにしても同じだから)
\(=-\displaystyle\frac{m}{a^2}\cdot\displaystyle\frac{1}{6}\cdot2a(2a+1)(4a+1)+\displaystyle\frac{2m}{a}\cdot\displaystyle\frac{1}{2}2a(2a+1)\)
\(=\displaystyle\frac{m}{3a}(4a^2-1)\)
ゆえに
\(\displaystyle\frac{m}{3a}(4a^2-1)<L_m≦\displaystyle\frac{m}{3a}(4a^2-1)+(2a+1)\)
(1)の結果から
\(\displaystyle\frac{4a^2-1}{4a^2}<\displaystyle\frac{L_m}{S_m}≦\displaystyle\frac{4a^2-1}{4a^2}+\displaystyle\frac{3(2a+1)}{4am}\)
\(\displaystyle\lim_{m \to \infty}\displaystyle\frac{3(2a+1)}{4am}=0\) だから、はさみうちの原理から
\(\displaystyle\lim_{m \to \infty}\displaystyle\frac{L_m}{S_m}=\displaystyle\frac{4a^2-1}{4a^2}\)
(参考)
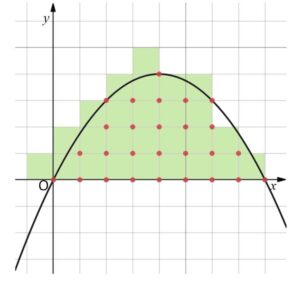
格子点の数\(1\)を、その格子点が右下の点になるような面積\(1\)の正方形に対応させると、正方形の全面積(格子点の全個数に対応)は図のようになります。\(m\)を大きくしていくと、グラフに対して相対的に正方形は小さくなるので、正方形の面積\(L_m\)とグラフと\(x\)軸で囲まれた面積\(S_m\)は近い値になっていきます。したがって\(\displaystyle\lim_{m \to \infty}\displaystyle\frac{L_m}{S_m}\)は\(1\)に近い値になります。(\(1\)になることもあります)
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→極限と正誤判定 back→はさみうちの原理③(ガウス記号)