無限級数の発散・収束にかんする例題です。
(例題1)
数列\(\{a_n\}\)の初項\(a_1\)から第\(n\)項までの和を\(S_n\)と表す。この数列が
\(a_1=1\), \(\displaystyle\lim_{n \to \infty}S_n=1\), \(n(n-2)a_{n+1}=S_n\) (\(n≧1\))
を満たすとき、一般項\(a_n\)を求めよ。
(解答)
\(n(n-2)a_{n+1}=S_n\)・・・① (\(n≧1\)) より
\((n-1)(n-3)a_{n}=S_{n-1}\)・・・② (\(n≧2\))
①-②から
\(n(n-2)a_{n+1}-(n-1)(n-3)a_{n}=a_{n}\) (\(n≧2\))
整理して
\(n(n-2)a_{n+1}=(n-2)^2a_{n}\)・・・③
(ア)\(n≧3\) のとき
③より
\(na_{n+1}=(n-2)a_n\)
(両辺で1つずれた形にするために\((n-1)\)を掛けて)
\(n(n-1)a_{n+1}=(n-1)(n-2)a_n\) (\(b_{n+1}=b_n\)の形)
よって
\((n-1)(n-2)a_n=(3-1)(3-2)a_3\)
ゆえに
\(a_n=\displaystyle\frac{2a_3}{(n-1)(n-2)}\)
(\(a_3\)を求めていきます。)
①より
\(S_n=n(n-2)\displaystyle\frac{2a_3}{n(n+1)}=\displaystyle\frac{n-2}{n+1}\cdot2a_3\)
\(\displaystyle\lim_{n \to \infty}S_n=1\) だから
\(1=2a_3\)
\(a_3=\displaystyle\frac{1}{2}\)
よって
\(a_n=\displaystyle\frac{1}{(n-1)(n-2)}\) (\(n≧3\))
(ii)\(n=2\) のとき
①で\(n=1\)として
\(-a_{2}=S_1\)
よって
\(a_2=\)\(-a_1=\)\(-1\)
以上から
\(a_1=1\), \(a_2=-1\)
\(a_n=\displaystyle\frac{1}{(n-1)(n-2)}\) (\(n≧3\))
(例題2)
正の数\(a\)に対して、数列\(\{x_n\}\)を
\(x_1=a\), \(x_{n+1}=x_n(1+x_n)\) (\(n=1,2,3,\cdots\))
によって定める。このとき
(1)\(\displaystyle\lim_{n \to \infty}x_n=\infty\) であることを示せ。
(2)無限級数 \(\displaystyle\sum_{n=1}^{\infty}\displaystyle\frac{1}{x_n+1}\) は収束することを示し、その和を求めよ。
(解答)
(1)
\(x_{n+1}=x_n(1+x_n)\) より
\(x_{n+1}-x_n=x_n^2\)・・・① (階差型)
①と\(x_1=a\ (>0)\)より帰納的に\(\{x_n\}\)は単調増加数列になるから \(x_n>a\)。
また、\(x_n,a\)は正の数だから \(x_n^2>a^2\)・・・②
①②より\(n≧2\)のとき
\(x_n=x_1+\displaystyle\sum_{k=1}^{n-1}x_k^2>x_1+\displaystyle\sum_{k=1}^{n-1}a^2\)
よって
\(x_n>a+a^2(n-1)\)
\(\displaystyle\lim_{n \to \infty}\{a+a^2(n-1)\}=\infty\) だから
\(\displaystyle\lim_{n \to \infty}x_n=\infty\)
(参考)
\(x_{n+1}=f(x_n)\) 型なので、グラフを考えても極限が分かります。
\(y=f(x)=x(1+x)\) とおいて、\(y=x\) とあわせて図示すると次の通りです。
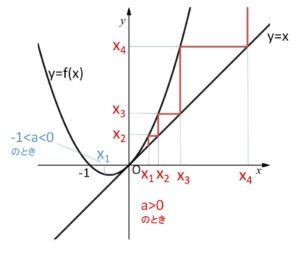
初項\(x_1=a\)は正の数で、\(x>0\) では \(y=f(x)\) のほうが上側にあるので、階段状の動きを追うと数列\(\{x_n\}\)が正の無限大に発散することが分かります。
また、例えば初項が \(-1<a<0\) の範囲にある場合は、同様に階段状の動きを追うことで2つのグラフの交点である原点に向かうことが分かるので、数列\(\{x_n\}\)は\(0\)に収束することが分かります。
(2)
(1)で \(x_n>0\) より
\(x_{n+1}=x_n(1+x_n)\) の逆数を取って
\(\displaystyle\frac{1}{x_{n+1}}=\displaystyle\frac{1}{x_n(1+x_n)}\)
(部分分数分解をして)
\(\displaystyle\frac{1}{x_{n+1}}=\displaystyle\frac{1}{x_n}-\displaystyle\frac{1}{1+x_n}\)
よって
\(\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{1+x_k}=\displaystyle\sum_{k=1}^{n}(\displaystyle\frac{1}{x_{k}}-\displaystyle\frac{1}{x_{k+1}})\)
(和において内側の項が打ち消されて)
\(=\displaystyle\frac{1}{x_{1}}-\displaystyle\frac{1}{x_{n+1}}\)
(1)より \(\displaystyle\lim_{n \to \infty}x_{n+1}=\infty\) だから
\(\displaystyle\sum_{n=1}^{\infty}\displaystyle\frac{1}{x_n+1}=\displaystyle\frac{1}{a}\) (収束する)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→無限等比級数① back→無限級数の収束・発散①