確率と極限に関する例題です。
(例題)
さいころを投げるという試行を繰り返し行う。ただし、2回連続して\(5\)以上の目が出た場合は、それ以降の試行は行わないものとする。
\(n\)回目の試行が行われ、かつ\(n\)回目に出た目が\(4\)以下になる確率を\(p_n\)とする。このとき、\(p_1=\displaystyle\frac{2}{3}\)、\(p_2=(\ 1\ )\)、\(p_3=(\ 2\ )\) である。また \(p_0=1\) とおく。\(n≧0\) に対して、\(p_n,p_{n+1},p_{n+2}\) の間に成立する関係式を求め、それを \(p_{n+2}-βp_{n+1}=α(p_{n+1}-βp_n)\) (\(α>β\)) の形に書くと \(α=(\ 3\ )\) である。よって、\(p_n=\displaystyle\frac{\sqrt{3}}{2}(\ 4\ )\) となる。
また、\(n\)回目の試行が行われ、かつ\(n\)回目に出た目が\(5\)以上になる確率を\(q_n\)とする。このとき、\(q_1=\displaystyle\frac{1}{3}\) である。\(n≧2\) とするとき、\(q_n\)と\(p_{n-1},p_{n-2}\)の間には \(q_n=(\ 5\ )\) なる関係式が成り立つ。したがって、\(\displaystyle\sum_{n=1}^{\infty}q_n=(\ 6\ )\) である。
\(n\)回目でちょうど試行が終わるときも、\(n\)回目の試行が行われていることには注意です。また、\(4\)以下の目が出るとそれ以前の目の出方はあまり関係ない、つまりリセットされるという状態になります。
(解答)
(1)
1回目にどの目が出ても2回目の試行は行われるから
\(p_2=\displaystyle\frac{2}{3}\)
(2)
3回目の試行が行われるには、1回目2回目で連続して\(5\)以上の目が出なければよい。
よって
\(p_3=\{1-(\displaystyle\frac{1}{3})^2\}\cdot(\displaystyle\frac{2}{3})\)\(=\displaystyle\frac{16}{27}\)
(3)
ちなみに、2項間漸化式にならないのは\(1-p_{n}\)の状態が、(ア)\(n\)回目の試行ができていて、5以上の目が出る (イ)\(n\)回目の試行ができてない(すでに終わってる状態) 場合があり、さらに(ア)では\(5\)以上の目が2回連続出ている場合と、そうでない場合に分けられて、漸化式が立式できないからです。後に出てくる\(q_n\)についても同じです。
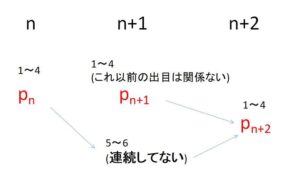
\(n+2\)回目の試行ができて、\(4\)以下の目が出るには
\(n+1\)回目に (i)\(4\)以下の目が出る (ii)\(5\)以上の目が出る
場合がある。(ii)の場合は\(5\)以上の目が連続して出てはいけないので、\(n\)回目に\(4\)以下の目が出ている必要がある。よって漸化式は次の通りになる。
\(p_{n+2}=p_{n+1}\cdot\displaystyle\frac{2}{3}+p_n\cdot\displaystyle\frac{1}{3}\cdot\displaystyle\frac{2}{3}\)・・・① (\(p_0=1\)とすれば \(n=0\)でも成り立つ)
(あとは整理して特性方程式を解くだけです)
①の特性方程式を解くと
\(x^2=\displaystyle\frac{2}{3}x+\displaystyle\frac{2}{9}\)
\(9x^2-6x-2=0\)
\(x=\displaystyle\frac{3±3\sqrt{3}}{9}=\displaystyle\frac{1±\sqrt{3}}{3}\)
\(α>β\) だから
\(α=\displaystyle\frac{1+\sqrt{3}}{3}\), \(β=\displaystyle\frac{1-\sqrt{3}}{3}\)
(4)
(3)より①は次のように変形できる。
\(p_{n+2}-βp_{n+1}=α(p_{n+1}-βp_n)\)・・・②
\(p_{n+2}-αp_{n+1}=β(p_{n+1}-αp_n)\)・・・③
②より
\(\color{blue}{p_{n+1}-βp_n}=α^{n}(p_1-βp_0)=\color{blue}{α^{n}(\displaystyle\frac{2}{3}-β)}\)・・・④
③より
\(\color{blue}{p_{n+1}-αp_n}=β^{n}(p_1-αp_0)=\color{blue}{β^{n}(\displaystyle\frac{2}{3}-α)}\)・・・⑤
④-⑤より
\((α-β)p_n=α^{n}(\displaystyle\frac{2}{3}-β)-β^{n}(\displaystyle\frac{2}{3}-α)\)
\(α,β\)に数値を代入して計算すると
\(\displaystyle\frac{2\sqrt{3}}{3}p_n=(\displaystyle\frac{1+\sqrt{3}}{3})^n(\displaystyle\frac{1+\sqrt{3}}{3})-(\displaystyle\frac{1-\sqrt{3}}{3})^n(\displaystyle\frac{1-\sqrt{3}}{3})\)
したがって
\(p_n=\displaystyle\frac{\sqrt{3}}{2}\left\{(\displaystyle\frac{1+\sqrt{3}}{3})^{n+1}-(\displaystyle\frac{1-\sqrt{3}}{3})^{n+1}\right\}\) (\(n≧0\))
(5)
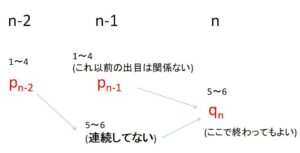
(3)と同様に
\(q_n=p_{n-1}\cdot\displaystyle\frac{1}{3}+p_{n-2}\cdot\displaystyle\frac{1}{3}\cdot\displaystyle\frac{1}{3}\)
よって
\(q_n=\displaystyle\frac{1}{3}p_{n-1}+\displaystyle\frac{1}{9}p_{n-2}\) (\(n≧2\))
(6)
\(q_n\)については、\(n≧2\) の制限があるので、\(q_1\) とそれ以外で分けます。
\(α,β\) どちらも絶対値が\(1\)より小さいから、\(\{p_n\}\)の無限級数は収束して
\(\displaystyle\sum_{n=1}^{\infty}q_n=q_1+\displaystyle\sum_{n=2}^{\infty}q_n\)
\(=\displaystyle\frac{1}{3}+\displaystyle\sum_{n=2}^{\infty}(\displaystyle\frac{1}{3}p_{n-1}+\displaystyle\frac{1}{9}p_{n-2})\)
\(=\displaystyle\frac{1}{3}+\displaystyle\sum_{n=1}^{\infty}\displaystyle\frac{1}{3}p_{n}+\displaystyle\sum_{n=0}^{\infty}\displaystyle\frac{1}{9}p_{n}\)
(計算しやすいように\(n=0\)スタートにします)
\(=\displaystyle\frac{1}{3}+(\displaystyle\sum_{n=0}^{\infty}\displaystyle\frac{1}{3}p_{n}-\displaystyle\frac{1}{3}p_0)+\displaystyle\sum_{n=0}^{\infty}\displaystyle\frac{1}{9}p_{n}\)
\(=\displaystyle\sum_{n=0}^{\infty}\displaystyle\frac{4}{9}p_{n}\) (\(p_0=1\) より)
\(=\displaystyle\sum_{n=0}^{\infty}\displaystyle\frac{4}{9}\cdot\displaystyle\frac{\sqrt{3}}{2}(α^{n+1}-β^{n+1})\)
\(=\displaystyle\frac{2\sqrt{3}}{9}(\displaystyle\frac{α}{1-α}-\displaystyle\frac{β}{1-β})\)
\(=\displaystyle\frac{2\sqrt{3}}{9}\cdot\displaystyle\frac{α-β}{(1-α)(1-β)}\)
\(=\displaystyle\frac{2\sqrt{3}}{9}\cdot\displaystyle\frac{\displaystyle\frac{2\sqrt{3}}{3}}{(\displaystyle\frac{2-\sqrt{3}}{3})\cdot(\displaystyle\frac{2+\sqrt{3}}{3})}\)
\(=\displaystyle\frac{\displaystyle\frac{4}{9}}{\displaystyle\frac{1}{9}}\)
\(=4\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→図形と極限 back→循環小数