図形と極限

図形に関する極限の例題です。

(例題1)
斜辺\(BC\)の長さが\(a\)、\(AB\)の長さが\(c\)の直角三角形\(ABC\)がある。図のように斜辺\(BC\)を\(n\)等分する点を\(M_1,M_2,\cdots,M_{n-1}\)とし、\(\displaystyle\sum_{k=1}^{n-1}AM_k^2=S_n\) とする。

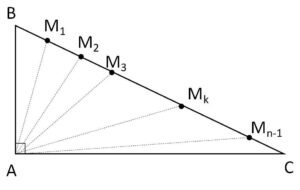
(1)\(S_n\)を求めよ。
(2)\(\displaystyle\lim_{n \to \infty}\displaystyle\frac{S_n}{n-1}\) を求めよ。

(解答)
(1)

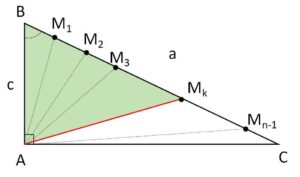
\(\cos B=\displaystyle\frac{c}{a}\),　\(BM_k=\displaystyle\frac{a}{n}k\)

よって余弦定理から
\(AM_k^2=c^2+(\displaystyle\frac{a}{n}k)^2-2\cdot c \cdot \displaystyle\frac{a}{n}k\cdot\displaystyle\frac{c}{a}\)

\(=\displaystyle\frac{a^2}{n^2}k^2-\displaystyle\frac{2c^2}{n}k+c^2\)

したがって
\(S_n=\displaystyle\sum_{k=1}^{n-1}AM_k^2\)

\(=\displaystyle\sum_{k=1}^{n-1}\left\{\displaystyle\frac{a^2}{n^2}k^2-\displaystyle\frac{2c^2}{n}k+c^2\right\}\)

\(=\displaystyle\frac{a^2}{n^2}\cdot\displaystyle\frac{1}{6}(n-1)n(2n-1)-\displaystyle\frac{2c^2}{n}\cdot\displaystyle\frac{1}{2}(n-1)n+c^2(n-1)\)

\(=\displaystyle\frac{a^2}{6n}(n-1)(2n-1)\)

(2)
\(\displaystyle\lim_{n \to \infty}\displaystyle\frac{S_n}{n-1}\)

\(=\displaystyle\lim_{n \to \infty}\displaystyle\frac{a^2(2n-1)}{6n}\)

\(=\displaystyle\lim_{n \to \infty}\displaystyle\frac{a^2(2-\displaystyle\frac{1}{n})}{6}\)

\(=\displaystyle\frac{2a^2}{6}\)

\(=\displaystyle\frac{1}{3}a^2\)

(例題2)
半直線 \(y=\sqrt{3}x\) (\(x≧0\)) と\(x\)軸に接する円の列\(O_n\) (\(n=1,2,3,\cdots\)) が図のように互いに接しながら並んでいる。円\(O_n\)の中心の座標を \((x_n,y_n)\) とし、面積を\(S_n\)とする。\(x_1=5\) のとき

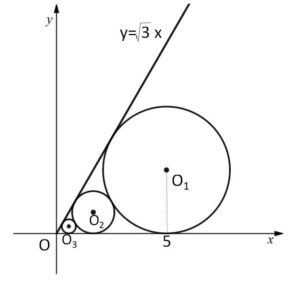
(1)\(y_1\)を求めよ。
(2)\(y_{n+1}\) を \(y_n\) を用いて表せ。
(3)\(\displaystyle\sum_{n=1}^{\infty}S_n\) を求めよ。

(解答)
(1)

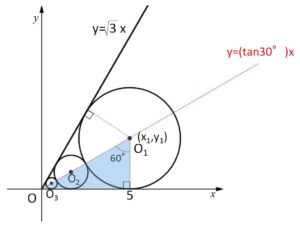
原点を通り、\(x\)軸と反時計回りに\(30°\)の角度をなす直線

\(y=\displaystyle\frac{1}{\sqrt{3}}x\)・・・①

上にすべての円の中心がある。よって円\(O_1\)の\(y\)座標\(y_1\)は
\(y_1=\displaystyle\frac{1}{\sqrt{3}}\cdot5=\)\(\displaystyle\frac{5\sqrt{3}}{3}\)

(別解)
円\(O_1\)の半径は\(y_1\ (>0)\)。円は \(\sqrt{3}x-y=0\) と接するから

\(\displaystyle\frac{|5\sqrt{3}-y_1|}{\sqrt{3+1}}=y_1\)

直線\(y=\sqrt{3}x\)の下側に円の中心\((5,y_1)\)があるから、\(y_1<5\sqrt{3}\)

よって
\(\displaystyle\frac{5\sqrt{3}-y_1}{2}=y_1\)
したがって
\(y_1=\displaystyle\frac{5\sqrt{3}}{3}\) (\(>0\)を満たす)

(2)

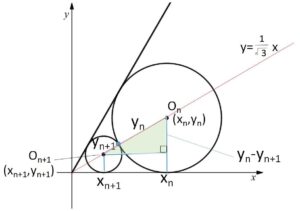
円\(O_n\)の半径は\(y_n\)だから、図の直角三角形において三平方の定理から
\((x_{n}-x_{n+1})^2+(y_{n}-y_{n+1})^2=(y_{n}+y_{n+1})^2\)・・・②

また円の中心は
\(y=\displaystyle\frac{1}{\sqrt{3}}x\)・・・①
にあるから
\(x_n=\sqrt{3}y_n\)・・・③

③を②に代入して
\((\sqrt{3}y_{n}-\sqrt{3}y_{n+1})^2+(y_{n}-y_{n+1})^2=(y_{n}+y_{n+1})^2\)
整理すると
\(3y_n^2-10y_ny_{n+1}+3y_{n+1}^2=0\)
\((3y_{n}-y_{n+1})(y_{n}-3y_{n+1})=0\)

図より \(y_{n}>y_{n+1}\) だから
\(3y_{n}-y_{n+1}≠0\)
したがって
\(y_{n}-3y_{n+1}=0\)
つまり
\(y_{n+1}=\displaystyle\frac{1}{3}y_n\)　(\(n=1,2,3,\cdots\))

(別解)点と直線の距離を利用すると
円\(O_n\)は \(\sqrt{3}x-y=0\) に接する。円\(O_n\)は、中心が \((x_{n},y_{n})\)、半径が \(y_n\) だから

\(\displaystyle\frac{|\sqrt{3}x_n-y_n|}{\sqrt{3+1}}=y_{n}\)

ここで、円の中心が直線 \(y=\sqrt{3}x\) より下側にあることから
\(y_n<\sqrt{3}x_n\)
つまり
\(\sqrt{3}x_n-y_n>0\)

よって
\(\displaystyle\frac{\sqrt{3}x_n-y_n}{2}=y_{n}\)
整理すると
\(y_n=\displaystyle\frac{1}{\sqrt{3}}x_n\)
となり、③と同じ式が導かれます。あとは三平方の定理を同様に利用するだけです。

(3)

(1)(2)より
\(y_{n+1}=\displaystyle\frac{1}{3}y_n\)
\(y_n=\displaystyle\frac{5\sqrt{3}}{3}\)

よって
\(y_n=\displaystyle\frac{5\sqrt{3}}{3}(\displaystyle\frac{1}{3})^{n-1}\)

円\(O_n\)の半径が\(y_n\)だから、その面積\(S_n\)は
\(S_n=πy_n^2\)

\(=\displaystyle\frac{25}{3}π\cdot(\displaystyle\frac{1}{9})^{n-1}\)　(等比数列)

したがって
\(\displaystyle\sum_{n=1}^{\infty}S_n\)\(=\displaystyle\frac{25}{3}π\cdot\displaystyle\frac{1}{1-\displaystyle\frac{1}{9}}\)

\(=\displaystyle\frac{25}{3}π\cdot\displaystyle\frac{9}{8}\)

\(=\displaystyle\frac{75}{8}π\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→ベクトルと極限　back→確率と極限