ベクトルと極限

ベクトルの極限に関する例題です。

(例題1)
座標平面において、点\(P_0\)を原点として、点\(P_1,P_2,P_3,\cdots\) を図のようにとっていく (点線は\(x\)軸と平行)。ただし、\(P_{n-1}P_n=\displaystyle\frac{1}{2^{n-1}}\) (\(n≧1\))、\(0<θ<\displaystyle\frac{π}{2}\) とする。

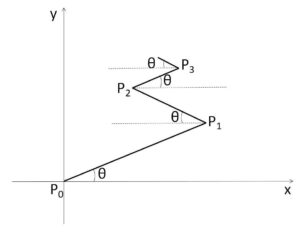
(1)\(P_0P_1+P_1P_2+\cdots+P_{n-1}P_n+\cdots\) を求めよ。
(2)\(P_n\)の座標を\(n\)と\(θ\)を用いて表せ。
(3)\(n\)を限りなく大きくするとき、点\(P_n\)はどのような点に近づくか。その点の座標を求めよ。

(解答)
(1)

(与式)
\(=1+\displaystyle\frac{1}{2}+\displaystyle\frac{1}{2^2}+\cdots\)
\(=\displaystyle\frac{1}{1-\displaystyle\frac{1}{2}}\)
\(=2\)

(2)

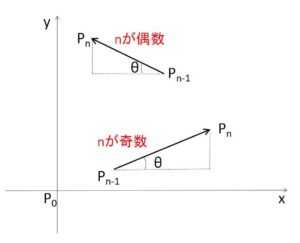
\(n\)が奇数のとき
\(\overrightarrow{P_{n-1}P_n}=\displaystyle\frac{1}{2^{n-1}}(\cosθ,\sinθ)\)

\(n\)が偶数のとき
\(\overrightarrow{P_{n-1}P_n}=\displaystyle\frac{1}{2^{n-1}}(-\cosθ,\sinθ)\)

(つまり、\(x\)成分の符号が交互に変わるだけ)

まとめると
\(\overrightarrow{P_{n-1}P_n}=\left((-\displaystyle\frac{1}{2})^{n-1}\cosθ,\ (\displaystyle\frac{1}{2})^{n-1}\sinθ\right)\)

よって\(P_n\)の座標はベクトルの和を考えて
\(\overrightarrow{P_{0}P_n}\)
\(=\overrightarrow{P_{0}P_1}+\overrightarrow{P_{1}P_2}+\cdots+\overrightarrow{P_{n-1}P_n}\)
\(=\left(\displaystyle\sum_{k=1}^{n}(-\displaystyle\frac{1}{2})^{k-1}\cosθ,\ \ \displaystyle\sum_{k=1}^{n}(\displaystyle\frac{1}{2})^{k-1}\sinθ\right)\)

\(=\left(\displaystyle\frac{1-(-\displaystyle\frac{1}{2})^{n}}{1+\displaystyle\frac{1}{2}}\cosθ,\ \displaystyle\frac{1-(\displaystyle\frac{1}{2})^{n}}{1-\displaystyle\frac{1}{2}}\sinθ\right)\)

したがって\(P_n\)の座標は
\(\left(\displaystyle\frac{2}{3}\left\{1-(-\displaystyle\frac{1}{2})^{n}\right\}\cosθ,\ 2\left\{1-(\displaystyle\frac{1}{2})^{n}\right\}\sinθ\right)\)

(3)

\(P_n(x_n,y_n)\) とおくと、(2)より

\((\displaystyle\lim_{n \to \infty}x_n,\displaystyle\lim_{n \to \infty}y_n)\)
\(=(\displaystyle\frac{2}{3}\cosθ,2\sinθ)\)

よって点\(P_n\)は、点\((\displaystyle\frac{2}{3}\cosθ,2\sinθ)\) に近づく。

(例題2)
\(xyz\)空間内の2直線
点\(O(0,0,0)\)を通り、\(\vec{l}=(1,1,1)\) に平行な直線\(l\)、
点\(A(0,1,0)\)を通り、\(\vec{m}=(2,3,-1)\) に平行な直線\(m\)
の上にそれぞれ点列 \(P_1,P_2,\cdots,P_n,\cdots\)、および \(Q_1,Q_2,\cdots,Q_n,\cdots\) があり、すべての\(n\)について線分\(P_nQ_n\)と直線\(m\)、線分\(Q_nP_{n+1}\)と直線\(l\)とはそれぞれ直交しているとする。\(n\)を限りなく大きくするとき、点\(P_n,Q_n\)はそれぞれどのような点に近づくか。

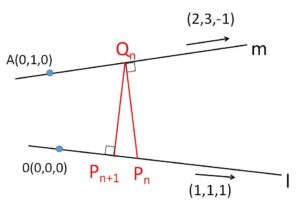
\(s,t\)を実数とすると直線\(l,m\)のベクトル方程式は

直線\(l\)
\(\vec{p}=(0,0,0)+s(1,1,1)=(s,s,s)\)

直線\(m\)
\(\vec{q}=(0,1,0)+t(2,3,-1)=(2t,3t+1,-t)\)

\(s=p_n\), \(t=q_n\) とおくと点\(P_n,Q_n\)は次のように表せる。
\(P_n=(p_n,p_n,p_n)\),　\(Q_n=(2q_n,3q_n+1,-q_n)\)

\(P_nQ_n \perp 直線m\) より
\((2q_n-p_n,\ 3q_n+1-p_n,\ -q_n-p_n)\cdot(2,3,-1)=0\)
整理すると
\(4p_n=14q_n+3\)・・・①

\(P_{n+1}Q_{n} \perp 直線l\) より
\((2q_{n}-p_{n+1},\ 3q_{n}+1-p_{n+1},\ -q_{n}-p_{n+1})\cdot(1,1,1)=0\)
整理すると
\(3p_{n+1}=4q_{n}+1\)・・・②

(連立漸化式①②を解く)
①より \(q_n=\displaystyle\frac{1}{14}(4p_n-3)\)・・・③

③を②に代入して整理すると
\(p_{n+1}=\displaystyle\frac{8}{21}p_n+\displaystyle\frac{1}{21}\)・・・④

特性方程式
\(x=\displaystyle\frac{8}{21}x+\displaystyle\frac{1}{21}\) を解くと
\(x=\displaystyle\frac{1}{13}\)

よって④は次のように変形できる。
\(p_{n+1}-\displaystyle\frac{1}{13}=\displaystyle\frac{8}{21}(p_n-\displaystyle\frac{1}{13})\)

ゆえに初項を\(p_1\)とおけば (このとき\(P_1(p_1,p_1,p_1)\)となる)
\(p_n=(\displaystyle\frac{8}{21})^{n-1}(p_1-\displaystyle\frac{1}{13})+\displaystyle\frac{1}{13}\)

したがって
\(\displaystyle\lim_{n \to \infty}p_n=\displaystyle\frac{1}{13}\)　(\(p_1\)に無関係)

また③より
\(\displaystyle\lim_{n \to \infty}q_n\)\(=\displaystyle\frac{1}{14}(4\cdot\displaystyle\frac{1}{13}-3)\)

\(=-\displaystyle\frac{5}{26}\)

よって点\(P_n,Q_n\)の極限は
\(\displaystyle\lim_{n \to \infty}P_n\)\(=\displaystyle\lim_{n \to \infty}(p_n,p_n,p_n)\)\(=(\displaystyle\frac{1}{13},\displaystyle\frac{1}{13},\displaystyle\frac{1}{13})\)

\(\displaystyle\lim_{n \to \infty}Q_n\)\(=\displaystyle\lim_{n \to \infty}(2q_n,3q_n+1,-q_n)\)\(=(-\displaystyle\frac{5}{13},\displaystyle\frac{11}{26},\displaystyle\frac{5}{26})\)

以上より、点\(P_n\)は点\((\displaystyle\frac{1}{13},\displaystyle\frac{1}{13},\displaystyle\frac{1}{13})\)に、点\(Q_n\)は点\((-\displaystyle\frac{5}{13},\displaystyle\frac{11}{26},\displaystyle\frac{5}{26})\)に近づく。

以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→(等差)×(等比)型の無限級数　back→図形と極限