指数・対数関数の極限(関数)

指数・対数関数の極限について見ていきます。

・指数・対数関数の極限
底が\(1\)より大きいか小さいかでグラフの形状が変わることと、対数関数 \(y=\log_ax\) の定義域が \(x>0\) であるから右側極限を考えることに注意するだけです。

\(a>0,\ a≠1\) とすると
指数関数 \(y=a^x\)、対数関数 \(y=\log_ax\) のグラフは\(a\)の値で分類すると次の通りです。\(a=\displaystyle\frac{1}{2},2\) などをイメージするとよいです。

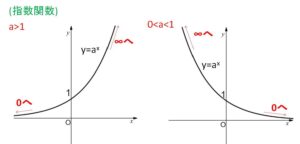
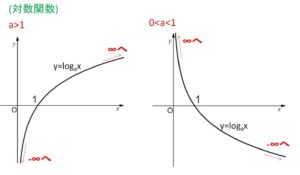
したがって
(1)指数関数
\(a>1\) のとき
\(\displaystyle\lim_{x \to \infty}a^x=\infty\)、\(\displaystyle\lim_{x \to -\infty}a^x=0\)

\(0<a<1\) のとき
\(\displaystyle\lim_{x \to \infty}a^x=0\)、\(\displaystyle\lim_{x \to -\infty}a^x=\infty\)

(2)対数関数
\(a>1\) のとき
\(\displaystyle\lim_{x \to \infty}\log_ax=\infty\)、\(\displaystyle\lim_{x \to +0}\log_ax=-\infty\)

\(0<a<1\) のとき
\(\displaystyle\lim_{x \to \infty}\log_ax=-\infty\)、\(\displaystyle\lim_{x \to +0}\log_ax=\infty\)

・対数関数・整式の関数(\(k\)次関数)・指数の関数の発散の強さ
対数関数・整式の関数・指数関数の発散について、次の等式が成り立ちます。

\(\displaystyle\lim_{x \to \infty}\displaystyle\frac{x}{2^x}=0\)、\(\displaystyle\lim_{x \to \infty}\displaystyle\frac{\log_2x}{x}=0\)　(底は\(1\)より大きければよい)

(解説)
つまり、対数関数<整式(\(k\)次関数)<指数関数 の順で発散のスピードが速くなるということです。
証明は、\(\displaystyle\lim_{x \to \infty}\displaystyle\frac{x}{2^x}=0\)・・・① については数列の極限の場合と同様に二項定理を用いますが、\(x\)は自然数であるとは限らないので\(x\)に近い自然数でワンクッションおいて(ガウス記号を使う)、はさみうちの原理を用いることになります。①が証明できたら、\(x=\log_2t\) と変換することでもう一方の等式が成り立つことが分かります。

まず①は
\([x]≦x\) より

\(\displaystyle\frac{x}{2^x}≦\displaystyle\frac{x}{2^{[x]}}\)・・・②

が成り立ち、右辺の分母\((1+1)^{[x]}\)で二項定理を用いて一部を取り出すと

\(\displaystyle\frac{x}{2^{[x]}}<\displaystyle\frac{x}{1+[x]+\displaystyle\frac{[x]([x]-1)}{2}}\)・・・③

よって②③より
\(0<\displaystyle\frac{x}{2^x}<\displaystyle\frac{1}{\displaystyle\frac{1}{x}+\displaystyle\frac{[x]}{x}+\displaystyle\frac{[x]}{x}\cdot\displaystyle\frac{[x]-1}{2}}\)

が成り立ち、\(\displaystyle\lim_{x \to \infty}\displaystyle\frac{[x]}{x}=1\) (ガウス記号の不等式とはさみうちの原理から証明できるが省略)、\(\displaystyle\lim_{x \to \infty}[x]=\infty\) より

\(\displaystyle\lim_{x \to \infty}\displaystyle\frac{x}{2^x}=0\)・・・①

さらに①で\(x=\log_2t\)とおくと \(x \to \infty\) のとき \(t \to \infty\) だから
\(\displaystyle\lim_{t \to \infty}\displaystyle\frac{\log_2t}{t}=0\)

なお、底を具体的に\(2\)に設定しましたが、\(1\)より大きい値ならよいです。底\(a\ (>1)\)について
\(a=1+h\)  (\(h>0\)) として同様に証明できます。さらに一般化すると整式(対数)の部分を\(k\)次式としても同様に\(0\)に収束します。つまり

\(\displaystyle\lim_{x \to \infty}\displaystyle\frac{x^k}{a^x}=0\)、\(\displaystyle\lim_{x \to \infty}\displaystyle\frac{(\log_ax)^k}{x}=0\)

です(同じく二項定理を用いて、変数変換すると示せる)。それほど指数と整式、整式と対数には発散のスピードに差があります。

(例題)次の極限値を求めよ。
(1)\(\displaystyle\lim_{x \to \infty}\{\displaystyle\frac{1}{2}\log_3x+\log_3(\sqrt{2x+1}-\sqrt{2x-1})\}\)

(2)\(\displaystyle\lim_{x \to \infty}\displaystyle\frac{(\displaystyle\frac{1}{2})^x-(\displaystyle\frac{1}{2})^{-x}}{(\displaystyle\frac{1}{2})^x+(\displaystyle\frac{1}{2})^{-x}}\)

(解答)
(1)
(対数の公式を用いて、真数の部分を1つにまとめると)
\(\displaystyle\lim_{x \to \infty}\{\displaystyle\frac{1}{2}\log_3x+\log_3(\sqrt{2x+1}-\sqrt{2x-1})\}\)

\(=\displaystyle\lim_{x \to \infty}\log_3\sqrt{x}(\sqrt{2x+1}-\sqrt{2x-1})\)

(有理化して)

\(=\displaystyle\lim_{x \to \infty}\log_3\displaystyle\frac{\sqrt{x}\{2x+1-(2x-1)\}}{\sqrt{2x+1}+\sqrt{2x-1}}\)

\(=\displaystyle\lim_{x \to \infty}\log_3\displaystyle\frac{2\sqrt{x}}{\sqrt{2x+1}+\sqrt{2x-1}}\)

\(=\displaystyle\lim_{x \to \infty}\log_3\displaystyle\frac{2}{\sqrt{2+\displaystyle\frac{1}{x}}+\sqrt{2-\displaystyle\frac{1}{x}}}\)

\(=\log_3\displaystyle\frac{2}{2\sqrt{2}}\)

\(=-\displaystyle\frac{1}{2}\log_32\)

(2)
\(\displaystyle\lim_{x \to \infty}\displaystyle\frac{(\displaystyle\frac{1}{2})^x-(\displaystyle\frac{1}{2})^{-x}}{(\displaystyle\frac{1}{2})^x+(\displaystyle\frac{1}{2})^{-x}}\)

\(=\displaystyle\lim_{x \to \infty}\displaystyle\frac{(\displaystyle\frac{1}{2})^x-2^x}{(\displaystyle\frac{1}{2})^x+2^x}\)

(\(2^x\)が一番強いのでこれで割る)

\(=\displaystyle\lim_{x \to \infty}\displaystyle\frac{(\displaystyle\frac{1}{2})^{2x}-1}{(\displaystyle\frac{1}{2})^{2x}+1}\)

\(=\displaystyle\frac{0-1}{0+1}\)

\(=-1\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→三角関数の極限①　back→関数の極限の基礎例題