はさみうちの原理を利用する関数の極限の例題です。
(例題)
\(a>0\)とする。このとき、3次方程式 \(\displaystyle\frac{1}{2}(x^3+3x)=a\) はただ1つの実数解 \(x(a)\ (>0)\) をもつ。正の数\(R\)に対し、\(0<a≦R\) の範囲で\(a\)を動かすとき、対応する実数解\(x(a)\)が整数となるような\(a\)の個数を\(N(R)\)とする。
(1)\(N(R)=1\) となるような\(R\)の範囲を求めよ。
(2)\(x=u-\displaystyle\frac{1}{u}\) とおくとき、\(\displaystyle\frac{1}{2}(x^3+3x)\) を\(u\)で表せ。また、\(x(a)\)を\(a\)で表せ。
(3)\(L=\displaystyle\lim_{R \to \infty}R^{-C}N(R)\) が有限な正の値となるとき、\(C\)の値を求めよ。また、このときの\(L\)の値を求めよ。
(解答)
(1)
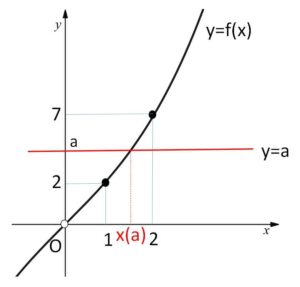
\(f(x)=\displaystyle\frac{1}{2}(x^3+3x)\) とおいて微分を用いると、グラフは図の通りになる。
\(y=f(x)\) と \(y=a\) の交点の\(x\)座標が\(x(a)\)であり、
\(f(1)=2\)、\(f(2)=7\)である。
\(0<a≦R\) の範囲でグラフ \(y=a\)を動かすので、\(N(R)=1\) となるような\(R\)の範囲は
\(2≦R<7\)
(\(R=7\)だと、\(x(a)=1,2\) の2個になるため含まない)
(2)
\(x=u-\displaystyle\frac{1}{u}\) より
\(\displaystyle\frac{1}{2}(x^3+3x)\)
\(=\displaystyle\frac{1}{2}\left\{(u-\displaystyle\frac{1}{u})^3+3(u-\displaystyle\frac{1}{u})\right\}\)
\(=\displaystyle\frac{1}{2}(u^3-\displaystyle\frac{1}{u^3})\)
これより、3次方程式 \(\displaystyle\frac{1}{2}(x^3+3x)=a\) は
\(\displaystyle\frac{1}{2}(u^3-\displaystyle\frac{1}{u^3})=a\)
となる。整理すると
\(u^6-2au^3-1=0\)
\((u^3)^2-2au^3-1=0\) (\(u^3\)の2次方程式とみる)
よって
\(u^3=a±\sqrt{a^2+1}\)
\(u=\sqrt[3]{a±\sqrt{a^2+1}}\)
(あとはこの\(u\)を代入して\(x\)を求めるだけです)
(ア)\(u=\sqrt[3]{a+\sqrt{a^2+1}}\) のとき
\(x=\sqrt[3]{a+\sqrt{a^2+1}}-\displaystyle\frac{1}{\sqrt[3]{a+\sqrt{a^2+1}}}\)
(イ)\(u=\sqrt[3]{a-\sqrt{a^2+1}}\) のとき
\(x=\sqrt[3]{a-\sqrt{a^2+1}}-\displaystyle\frac{1}{\sqrt[3]{a-\sqrt{a^2+1}}}\)
(\(\displaystyle\frac{1}{a-\sqrt{a^2+1}}=\displaystyle\frac{a+\sqrt{a^2+1}}{a^2-(a^2+1)}=-(a+\sqrt{a^2+1})\) より)
\(=-\displaystyle\frac{1}{\sqrt[3]{a+\sqrt{a^2+1}}}+\sqrt[3]{a+\sqrt{a^2+1}}\) ((ア)と同じになる)
したがって
\(x(a)=\sqrt[3]{a+\sqrt{a^2+1}}-\displaystyle\frac{1}{\sqrt[3]{a+\sqrt{a^2+1}}}\)
(3)
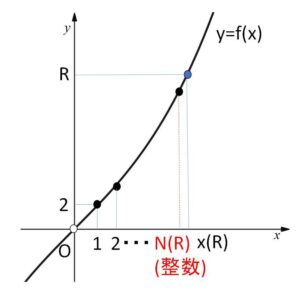
\(x(R)\)の整数部分が\(N(R)\)となるから
\(N(R)≦x(R)<N(R)+1\)
よって
\(x(R)-1<N(R)≦x(R)\)
\(R^{-C}(x(R)-1)<R^{-C}N(R)≦R^{-C}x(R)\)
(2)より
(左辺)
\(=R^{-C}\left(\sqrt[3]{R+\sqrt{R^2+1}}-\displaystyle\frac{1}{\sqrt[3]{R+\sqrt{R^2+1}}}-1\right)\)
\(=R^{\frac{1}{3}-C}\left(\displaystyle\frac{1}{\sqrt[3]{R}}\cdot\sqrt[3]{R+\sqrt{R^2+1}}-\displaystyle\frac{1}{\sqrt[3]{R}\sqrt[3]{R+\sqrt{R^2+1}}}-\displaystyle\frac{1}{\sqrt[3]{R}}\right)\)
\(=R^{\frac{1}{3}-C}\left(\sqrt[3]{1+\sqrt{1+\displaystyle\frac{1}{R^2}}}-\displaystyle\frac{1}{\sqrt[3]{R}\sqrt[3]{R+\sqrt{R^2+1}}}-\displaystyle\frac{1}{\sqrt[3]{R}}\right)\)
同様に
(右辺)
\(=R^{\frac{1}{3}-C}\left(\sqrt[3]{1+\sqrt{1+\displaystyle\frac{1}{R^2}}}-\displaystyle\frac{1}{\sqrt[3]{R}\sqrt[3]{R+\sqrt{R^2+1}}}\right)\)
ここで\(R \to \infty\)のとき、(左辺)、(右辺)のどちらも括弧内は\(\sqrt[3]{2}\)に収束するから、\(R^{\frac{1}{3}-C}\) が\(0\)でない正の有限値に収束すればよい。
\(C>\displaystyle\frac{1}{3}\) のとき \(\displaystyle\lim_{R \to \infty}R^{\frac{1}{3}-C}=\displaystyle\lim_{R \to \infty}\displaystyle\frac{1}{R^{C-\frac{1}{3}}}=0\)
\(C<\displaystyle\frac{1}{3}\) のとき \(\displaystyle\lim_{R \to \infty}R^{\frac{1}{3}-C}=\infty\)
\(C=\displaystyle\frac{1}{3}\) のとき \(\displaystyle\lim_{R \to \infty}R^{\frac{1}{3}-C}=\displaystyle\lim_{R \to \infty}1=1\)
だから、\(C=\displaystyle\frac{1}{3}\)
またこのとき
\(L=\displaystyle\lim_{R \to \infty}R^{-C}N(R)=\sqrt[3]{2}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→関数の連続・不連続 back→極限と条件式