今回からのテーマは2次関数です。数学Ⅰの重要テーマの1つなのでしっかり学習しましょう。
・関数とは
変数\(x\)の値を定めると、変数\(y\)の値がただ1つ定まるとき、「\(y\)は\(x\)の関数」であるといい、\(y=f(x)\)などで表されます。
\(y=2x+5\) (1次関数)
\(y=-x^2\) (2次関数)
\(y^2=x\)
\(y^2=x^2\) など
・2次関数
\(x\)の2次式で表される関数を\(x\)の2次関数といいます。一般に2次関数は次の形(一般形)で書き表されます。
\(y=ax^2+bx+c\) (\(a,b,c\)は定数で、\(a≠0\))
・2次関数のグラフ
\(y=ax^2+bx+c\)のグラフを描くには、まず \(y=ax^2\) のグラフを考えてみます。これは頂点が原点\((0,0)\)で、軸が\(y\)軸の放物線ですね。次に \(y=a(x-p)^2+q\) のグラフを考えます。頂点はグラフの最小値(または最大値)をとる座標なので、例えば\(a>0\)の場合には \((x-p)^2≧0\) から、\(x=p\)のとき\(y\)は最小値\(q\)をとることから、 \(y=a(x-p)^2+q\) の頂点は\((p,q)\)となります。このグラフの形状は \(y=ax^2\) と同じことから、 \(y=a(x-p)^2+q\) のグラフは \(y=ax^2\) のグラフを、「\(x\)軸方向に\(p\)、\(y\)軸方向に\(q\)」だけ平行移動したものになります。(正確には →グラフの平行移動 の考え方を利用します) よって、 \(y=ax^2+bx+c\) のグラフを描くにはこの式をうまく \(y=a(x-p)^2+q\) の形に変形すればよいですね。 \(y=a(x-p)^2+q\) の形を2次関数の標準形といいます。
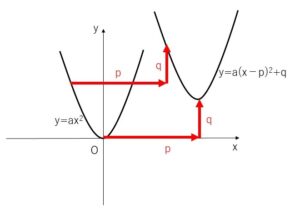
\(y=a(x-p)^2+q\)
\(y=ax^2\)を「\(x\)軸方向に\(p\)、\(y\)軸方向に\(q\)」だけ平行移動
・頂点 \((p,q)\)
・軸 \(x=p\)
2乗の形をうまくつくっていきます。(平方完成)
・軸 \(x=-\displaystyle\frac{b}{2a}\)
・頂点 \((-\displaystyle\frac{b}{2a},-\displaystyle\frac{b^2-4ac}{4a})\)
ちなみに\(a>0\)のときは、\(y=ax^2+bx+c\) のグラフは\(y=ax^2\)のグラフを、平行移動したものになるので、下に出っ張った形になります(下に凸)。\(a<0\)のときは上に出っ張った形です(上に凸)。
例題をやってみます。
(例題)
\(y=2x^2-6x+1\)のグラフを書いて、頂点の座標と軸の方程式を求めよ。
(解答)
上の方法と同様に平方完成していきます。
\(y=2(x^2-3x)+1\)
\(=2\{x^2-3x+(\displaystyle\frac{3}{2})^2-(\displaystyle\frac{3}{2})^2\}-1\)
\(=2(x-\displaystyle\frac{3}{2})^2-2(\displaystyle\frac{3}{2})^2+1\)
\(=2(x-\displaystyle\frac{3}{2})^2-\displaystyle\frac{7}{2}\)
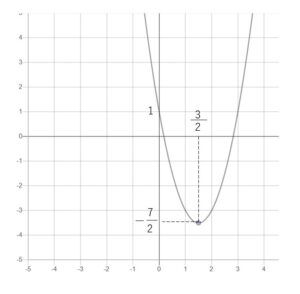
頂点 \((\displaystyle\frac{3}{2},-\displaystyle\frac{7}{2})\)
軸 \(x=\displaystyle\frac{3}{2}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。