前回、2次関数が与えられているときグラフを描くことを学びましたが、逆にグラフが与えられているときの関数式の係数の符号を調べていきます。
(問題)
2次関数 \(y=ax^2+bx+c\)のグラフが次の図で表されているとき、以下の値の符号を調べよ。
(1) \(a\) (2) \(b\) (3) \(c\) (4) \(b^2-4ac\) (5) \(a-b+c\)
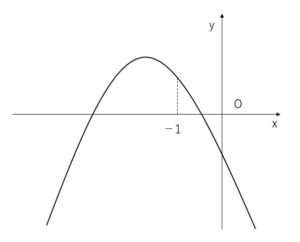
(解答)
グラフから頂点の座標の符号や、軸の方程式の係数の符号が分かるのでひとまず平方完成しておきます。(平方完成は →(1-1)関数の基礎と2次関数の基本形 を参照してください)
\(y=ax^2+bx+c=\)・・・
\(=a(x+\displaystyle\frac{b}{2a})^2-\displaystyle\frac{b^2-4ac}{4a}\)
(1)
グラフは上に凸なので \(a<0\)
(2)
軸が負の部分にあるので、 \(-\displaystyle\frac{b}{2a}<0\)
(1)の\(a<0\)から \(b<0\)
(3)
\(x=0\)を代入すると、\(y=c\) つまり\(c\)はグラフの\(y\)切片。
よって \(c<0\)
(4)
頂点の\(y\)座標は正。よって \(-\displaystyle\frac{b^2-4ac}{4a}>0\)
(1)の\(a<0\)から \(b^2-4ac>0\)
(5)
\(x=-1\)を代入すると、 \(y=a-b+c\) つまり \(a-b+c\) は\(x=-1\)における\(y\)座標。よって \(a-b+c>0\)
以上です。お疲れ様でした。
ここまで読んで頂きありがとうございました。