ある2次関数のグラフを平行移動すると、方程式はどのような形に変化するか見ていきます。
・2次関数のグラフの平行移動
\(y=ax^2\) のグラフを \(x\)軸方向に\(p\), \(y\)軸方向に\(q\)だけ平行移動したグラフを考えていきます。まず \(y=ax^2\) 上の点を\((X,Y)\)とおいて、\((X,Y)\)を\(x\)軸方向に\(p\), \(y\)軸方向に\(q\)移動した点を(\(x,y\))とします。
求めたい式は\(x,y\)の関係式です。まず\((X,Y)\)は \(y=ax^2\) 上にあるので、\(Y=aX^2\)・・・① 次に、\((X,Y)\)を\(x\)軸方向に\(p\), \(y\)軸方向に\(q\)移動した点を(\(x,y\))としたので、\(x=X+p\)・・・② \(y=Y+q\)・・・③ ②③を変形して、\(X=x-p\)・・・④ \(Y=y-q\)・・・⑤ ④⑤を①に代入して、\(y-q=a(x-p)^2\) これが平行移動後の方程式となります。
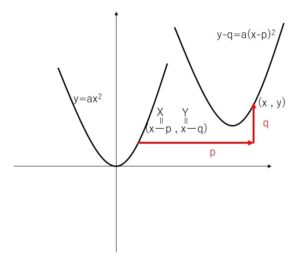
同様に考えると、\(y=ax^2+bx+c\)を \(x\)軸方向に\(p\), \(y\)軸方向に\(q\)だけ平行移動したグラフの方程式は、\(y-q=a(x-p)^2+b(x-p)+c\) となります。
つまり \(x→x-p\) \(y→y-q\) と置き換えればよいことが分かります。
\(p,q\)移動だから \(x→x+p\) \(y→y+q\) とはならないことに注意してください。
(例題1)
\(y=x^2-4x+3\)を「\(x\)軸方向に\(3\), \(y\)軸方向に\(-1\)」だけ平行移動した曲線の方程式を求めよ。
\(y=x^2-4x+3\)を「\(x\)軸方向に\(3\), \(y\)軸方向に\(-1\)」だけ平行移動した曲線の方程式を求めよ。
(解答)
移動後の曲線の方程式は
\(y-(-1)=(x-3)^2-4(x-3)+3\)
整理して
\(y=x^2-10x+23\)
移動後の曲線の方程式は
\(y-(-1)=(x-3)^2-4(x-3)+3\)
整理して
\(y=x^2-10x+23\)
(例題2)
ある放物線\(C\)を,\(x\)軸方向に\(2\), \(y\)軸方向に\(1\)だけ平行移動すると、放物線 \(y=2x^2-3x+4\) となった。放物線\(C\)の方程式を求めよ。
ある放物線\(C\)を,\(x\)軸方向に\(2\), \(y\)軸方向に\(1\)だけ平行移動すると、放物線 \(y=2x^2-3x+4\) となった。放物線\(C\)の方程式を求めよ。
(解答)
反対に考えると、\(y=2x^2-3x+4\) を\(x\)軸方向に\(-2\), \(y\)軸方向に\(-1\)だけ平行移動すると\(C\)となるので
\(C: y+1=2(x+2)^2-3(x+2)+4\)
整理すると
\(C: y=2x^2+5x+5\)
反対に考えると、\(y=2x^2-3x+4\) を\(x\)軸方向に\(-2\), \(y\)軸方向に\(-1\)だけ平行移動すると\(C\)となるので
\(C: y+1=2(x+2)^2-3(x+2)+4\)
整理すると
\(C: y=2x^2+5x+5\)
放物線とは物を投げたときに描く曲線のことです。物理の話になりますが、放物線の方程式は2次関数となります。
・一般的な曲線の平行移動
一般的な関数 \(y=f(x)\) を \(x\)軸方向に\(p\), \(y\)軸方向に\(q\)だけ平行移動した曲線の方程式は、
\(y-q=f(x-p)\)
となります。証明は2次関数の平行移動とほぼ同じなので簡単にします。
\(y-q=f(x-p)\)
となります。証明は2次関数の平行移動とほぼ同じなので簡単にします。
\(y=f(x)\)上の点を\((X,Y)\)、この点の平行移動後の座標を\((x,y)\)とおく。
\(Y=f(X)\)・・・① \(x=X+p\)・・・② \(y=Y+q\)・・・③
①~③より \(y-q=f(x-p)\)
\(Y=f(X)\)・・・① \(x=X+p\)・・・② \(y=Y+q\)・・・③
①~③より \(y-q=f(x-p)\)
以上になります。お疲れさまでした。
ここまで読んで頂きありがとうございました。
ここまで読んで頂きありがとうございました。