前回紹介した基本的な知識と2次関数のグラフの性質を利用して、2次関数の決定の他のパターンの問題について見ていきましょう。
(問題1)
放物線 \(y=-x^2\) を平行移動したもので、点\((1,3)\)を通り、頂点が直線 \(y=2x+1\)上にある2次関数を求めよ。
まず平行移動しても \(x^2\)の係数は変わらないことを示しておきます。標準形 \(y=a(x-p)^2+q\)で、「\(x\)軸方向に\(m\),\(y\)軸方向に\(n\)」だけ平行移動した放物線の方程式は、\(y-n=a(x-m-p)^2\) 移動前後で\(x^2\)の係数は\(a\)のままなので、変化していません。任意の2次関数は標準形に変形することができるので、任意の2次関数を平行移動しても\(x^2\)の係数は変わりません。
(解答)
問題文より頂点の座標を\((p,2p+1)\)とおく。
求める2次関数の\(x^2\)の係数は\(-1\)だから
\(y=-(x-p)^2+2p+1\)・・・①が求める放物線である。
\((1,3)\)を代入して
\(3=-(1-p)^2+2p+1\)
整理して、\(p^2-4p+3=0\)
これから、\(p=1,3\)
(ア)\(p=1\)のとき
①より \(y=-(x-1)^2+3\)
(イ)\(p=3\)のとき
①より \(y=-(x-3)^2+7\)
問題文より頂点の座標を\((p,2p+1)\)とおく。
求める2次関数の\(x^2\)の係数は\(-1\)だから
\(y=-(x-p)^2+2p+1\)・・・①が求める放物線である。
\((1,3)\)を代入して
\(3=-(1-p)^2+2p+1\)
整理して、\(p^2-4p+3=0\)
これから、\(p=1,3\)
(ア)\(p=1\)のとき
①より \(y=-(x-1)^2+3\)
(イ)\(p=3\)のとき
①より \(y=-(x-3)^2+7\)
以上から、\(y=-(x-1)^2+3\) または \(y=-(x-3)^2+7\)
(問題2)
次の条件を満たす\(x\)の2次関数を求めよ。
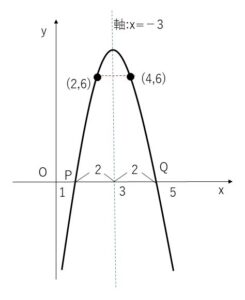
・2点 \((2,6),(4,6)\) を通り、\(x\)軸と2点\(P,Q\)で交わり、\(PQ=4\)である。
次の条件を満たす\(x\)の2次関数を求めよ。
・2点 \((2,6),(4,6)\) を通り、\(x\)軸と2点\(P,Q\)で交わり、\(PQ=4\)である。
(解答)
2点の\(y\)座標が同じことに着目して、\(x\)の2次関数上の\(y\)座標が同じ2点は、軸について対称な点どうしであることを利用します。
・2点\((2,6),(4,6)\)は\(y\)座標が同じで、軸について対称な点どうしであるから、求める放物線の軸は、2点\((2,6),(4,6)\)の中点(\(3,6\))を通り、\(x\)軸に垂直な直線なので、軸は\(x=3\)
\(P,Q\)はともに\(y\)座標が0なので、\(P,Q\)も軸に対称な点どうし。よって\(P,Q\)は\((3,0)\)から距離 \(4÷2=2\) の\(x\)軸上の点であり、それぞれ \((1,0),(5,0)\)
よって求める2次関数は
\(y=a(x-1)(x-5)\)とおけ、\((2,6)\)を通るので
\(6=-3a\) ゆえに\(a=-2\)
したがって 求める2次関数は
\(y=-2(x-1)(x-5)\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。