まずは簡単な1次関数の問題について考えていきます。
(問題)
1次関数\(y=ax+b\)について、定義域を(\(-1≦x≦3\))とする。\(y\)の最大値が\(4\)、最小値が\(-1\)のとき、定数\(a,b\)の値を求めよ。
(解答)
(ア)\(a>0\)のとき
単調増加関数なので
最大値は\(x=3\)、最小値は\(x=-1\)の場合で
\(3a+b=4\) \(-a+b=-1\)
\(a,b\)について解くと
\(a=\displaystyle\frac{5}{4}\) \(b=\displaystyle\frac{1}{4}\)
(\(a>0\)を満たす)
(イ)\(a<0\)のとき
単調減少関数なので
最大値は\(x=-1\)のとき、最小値は\(x=3\)のときで
\(-a+b=4\) \(3a+b=-1\)
\(a,b\)について解くと
\(a=-\displaystyle\frac{5}{4}\) \(b=\displaystyle\frac{11}{4}\)
(\(a<0\)を満たす)
・定義域によって式が違う関数
続いて、定義域で関数の式が違う場合について考えていきます。
(例)
\(
\begin{eqnarray}
f(x)
=
\begin{cases}
-x+2 & (1≦x≦2) \\
x^2 & (-2≦x<1)
\end{cases}
\end{eqnarray}
\)
(1)グラフをかけ (2)グラフの最大値、最小値およびそのときの\(x\)の値を求めよ。
(解答)
(1)グラフは以下のとおり。
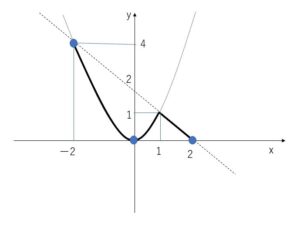
(2)グラフより
最大値は\(4\) (\(x=-2\))
最小値は\(0\) (\(x=0,2\))
以上になります。お疲れさまでした。
ここまで読んで頂きありがとうございました。