絶対値を含む1次関数のグラフはどのような形になるか見ていきます。
(例1)
\(y=|x-2|\) のグラフをかけ。
絶対値の中身の正負で場合分けです。
(1) \(x-2<0\) つまり \(x<2\) のとき
\(y=-(x-2)=-x+2\)
(2) \(x-2≧0\) つまり \(x≧2\)のとき
\(y=x-2\)
\(y=-(x-2)=-x+2\)
(2) \(x-2≧0\) つまり \(x≧2\)のとき
\(y=x-2\)
(1)(2)をグラフにすると
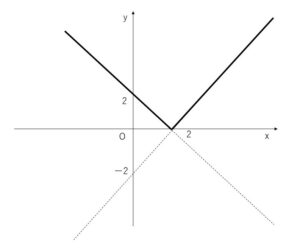
\(|x-2|\)の絶対値を外すときは、中身が正の場合はそのまま、負の場合は-をつけるだけなので、\(y=|x-2|\) のグラフは、\(y=x-2\)のグラフの正の部分はそのままで、負の部分は\(x\)軸について折り返したものを合わせた形になります。
(例2)
\(y=|x+3|+|x-1|\) のグラフをかけ。
\(y=|x+3|+|x-1|\) のグラフをかけ。
1つの目の絶対値の中身の正負の境目は \(x=-3\) で 2つ目は \(x=1\)です。①\(x<-3\) ② \(-3≦x<1\) ③ \(x≧1\) の3つに場合分けします。
①\(x<-3\)のとき
\(y=-(x+3)-(x-1)=-2x-2\)
②\(-3≦x<1\)のとき
\(y=x+3-(x-1)=4\)
③\(x≧1\)のとき
\(y=x+3+x-1=2x+2\)
\(y=-(x+3)-(x-1)=-2x-2\)
②\(-3≦x<1\)のとき
\(y=x+3-(x-1)=4\)
③\(x≧1\)のとき
\(y=x+3+x-1=2x+2\)
以上①~③をグラフにすると
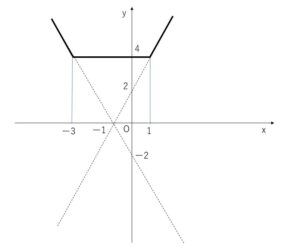
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
ここまで見て頂きありがとうございました。