文字定数を含む2つの2次方程式が与えられたときに、両方の2次方程式が実数解をもつ場合や、片方のみが実数解をもつ場合などについて考えていきます。
(問題)
2つの2次方程式
\(x^2-x+a=0\)・・・① \(x^2+2ax-3a+4=0\)・・・②
について次の条件を満たす定数\(a\)の値の範囲を求めよ。
(1)両方とも実数解をもつ (2)少なくとも一方が実数解をもたない
(3)一方だけが実数解をもつ
それぞれの方程式の判別式の符号を検討していきます。
(解答)
①の判別式を\(D_1\)、②の判別式を\(D_2\)とすると
\(D_1=1-4a\)
\(\displaystyle\frac{D_2}{4}=a^2+3a-4=(a+4)(a-1)\)
(1)両方とも実数解をもつ条件は、\(D_1≧0\) かつ \(D_2≧0\)
\(D_1≧0\) を解くと \(1-4a≧0\) より \(a≦\displaystyle\frac{1}{4}\)・・・③
\(D_2≧0\) を解くと \((a+4)(a-1)≧0\) より
\(a≦-4\) または \(a≧1\)・・・④
③④を数直線上に図示すると以下のようになる。
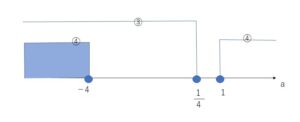
したがって求める\(a\)の値の範囲は \(a≦-4\)
③かつ④なので、両方を満たす範囲つまり共通部分になります。
(2)
少なくとも一方が実数解をもたないということは、最低片方が実数解をもたなければいいので、\(D_1<0\) または \(D_2<0\) となります。この中には両方実数解をもたない場合も含まれます。
少なくとも一方が実数解をもたない条件は、\(D_1<0\) または \(D_2<0\)
\(D_1<0\) を解くと \(1-4a<0\) より \(a>\displaystyle\frac{1}{4}\)・・・⑤
\(D_2<0\) を解くと \((a+4)(a-1)<0\) より \(-4<a<1\)・・・⑥
\(D_2<0\) を解くと \((a+4)(a-1)<0\) より \(-4<a<1\)・・・⑥
⑤⑥を数直線上に図示すると以下のようになる。
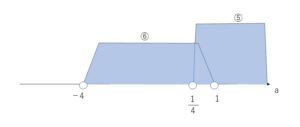
したがって求める\(a\)の範囲は、\(a>-4\)
⑤または⑥なので、2つを合わせた範囲となります。
(3)
一方のみが実数解をもつ(もう片方は実数解をもたない)ので、「\(D_1≧0\)かつ\(D_2<0\)」 または 「\(D_1<0\)かつ\(D_2≧0\)」となりますが、面倒なので(1)の数直線を利用して片方だけ成り立つ範囲を調べます。
求める条件は、\(D_1≧0\) と \(D_2≧0\) の一方のみが成り立つ\(a\)の範囲である。
(1)の数直線を利用すると、一方のみが成り立つ\(a\)の範囲は次図の色付きの部分となる。
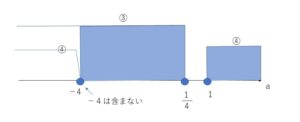
したがって求める\(a\)の範囲は
\(-4<a≦\displaystyle\frac{1}{4}\) または \(a≧1\)
\(-4<a≦\displaystyle\frac{1}{4}\) または \(a≧1\)
\(a=-4\)のときは、\(D_1≧0\) と \(D_2≧0\) の両方が成り立つので含めません。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。