2つの2次不等式の両方を満たす解を考えていきます。それぞれの2次不等式を解いて共通部分を調べるだけなのでそれほど難しくはありません。
(例題)次の2つの不等式をともに満たす\(x\)の範囲を求めよ。
\(x^2-2x-1≧0\)・・・① \(x^2-x-6<0\)・・・②
(解答)
①について \(x^2-2x-1=0\)を解くと
\(x=1±\sqrt{2}\)から ①の解は
\(x≦1-\sqrt{2}\) または \(x≧1+\sqrt{2}\)・・・③
②について与式は \((x+2)(x-3)<0\) となり
②の解は \(-2<x<3\)・・・④
③、④を数直線上に図示すると、以下のようになる。
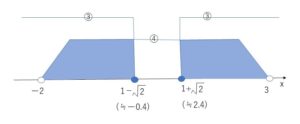
\(\sqrt{2}≒1.4\)なので、\(1-\sqrt{2}≒-0.4\)、\(1+\sqrt{2}≒2.4\)です。
よって 求める解は、
\(-2<x≦1-\sqrt{2}\) または \(1+\sqrt{2}≦x<3\)
③の2つの範囲はどちらでもよいので、③と④の両方を満たす\(x\)、つまり③かつ④の\(x\)の範囲は、色付きの部分2つになります。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。