文字係数の2次不等式を解く場合は、係数が数字のみの2次不等式を解く方法と基本的には変わりません。まずは、2次関数のグラフと\(x\)軸と交わるのかどうか、交わった場合その\(x\)座標はどうなるか考えます。要するにグラフと\(x\)軸の位置関係を調べます。
(例題1)
\(x\)についての2次不等式 \(x^2-2ax-2x+4a≦0\) を解け。
\(y=\)(左辺) とおいたときのグラフと\(x\)軸の位置関係を調べますが、とりあえず因数分解できるかどうか試してみます。因数分解できればグラフと\(x\)軸は共有点をもつことになります。
(解答)
左辺を因数分解すると
\((x-2a)(x-2)≦0\)・・・①
\(x\)軸との共有点の\(x\)座標が、\(x=2a,2\)ですが、\(2a\)と\(2\)の大小で解が変わってきますので、場合分けします。
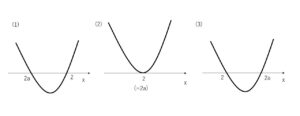
(1)\(2a<2\) つまり \(a<1\)のとき
①の解は \(2a≦x≦2\)
①の解は \(2a≦x≦2\)
(2)\(2a=2\) つまり \(a=1\)のとき
①は \((x-2)^2≦0\)
よって①の解は \(x=2\)
①は \((x-2)^2≦0\)
よって①の解は \(x=2\)
(3)\(2a>2\) つまり \(a>1\)のとき
①の解は \(2≦x≦2a\)
①の解は \(2≦x≦2a\)
(例題2)
次の不等式を解け。ただし\(a\)は定数とする。
\(ax^2≦ax\)
次の不等式を解け。ただし\(a\)は定数とする。
\(ax^2≦ax\)
(解答)
与式より
\(ax^2-ax≦0\)
\(ax(x-1)≦0\)・・・①
与式より
\(ax^2-ax≦0\)
\(ax(x-1)≦0\)・・・①
両辺を\(a\)で割れば文字\(a\)は消えますが、正・負(不等号の向きが変わる)で場合分けします。\(a=0\)の場合は割ってはいけないので別に考えます。
(1)\(a>0\)のとき
①の両辺を\(a\)で割ると
\(x(x-1)≦0\)
よって①の解は \(0≦x≦1\)
①の両辺を\(a\)で割ると
\(x(x-1)≦0\)
よって①の解は \(0≦x≦1\)
(2)\(a=0\)のとき
①は \(0・x(x-1)≦0\) でどのような\(x\)を代入しても不等式\(0≦0\)は成り立つ。
よって①の解は すべての実数
①は \(0・x(x-1)≦0\) でどのような\(x\)を代入しても不等式\(0≦0\)は成り立つ。
よって①の解は すべての実数
(3)\(a<0\)のとき
①の両辺を\(a\)で割ると
\(x(x-1)\)\(≧\)\(0\)
よって①の解は \(x≦0,x≧1\)
①の両辺を\(a\)で割ると
\(x(x-1)\)\(≧\)\(0\)
よって①の解は \(x≦0,x≧1\)
以上になります。お疲れさまでした。
ここまで読んで頂きありがとうございました。