2次不等式の解が与えられているとき、2次式の係数を決定する方法について見ていきましょう。
(例題)
\(x\)についての2次不等式 \(ax^2+9x+2b>0\)の解が、\(4<x<5\) となるように、\(a,b\)の値を定めよ。
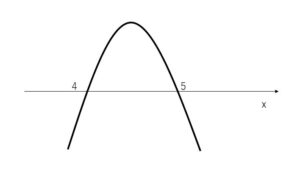
グラフが\(x\)軸より上側にある範囲が \(4<x<5\) なので、グラフは上に凸で、\(a<0\)です。下に凸のグラフの方針を貫いて、\(ax^2+9x+2b>0\)の両辺に\(-1\)をかけて \(-ax^2-9x-2b<0\) の解が \(4<x<5\) (下に凸のグラフで\(-a>0\))としてもよいですが、ややこしくなりそうなので、上に凸のグラフで考えていきます。
(解答)
\(y=f(x)=ax^2+9x+2b\) のグラフが、\(4<x<5\)のときだけ\(x\)軸の上方にある条件なので \(a<0\)。また \(f(4)=0,f(5)=0\) なので、
\(y=f(x)=ax^2+9x+2b\) のグラフが、\(4<x<5\)のときだけ\(x\)軸の上方にある条件なので \(a<0\)。また \(f(4)=0,f(5)=0\) なので、
\(f(4)=16a+36+2b=0\)・・・①
\(f(5)=25a+45+2b=0\)・・・②
\(f(5)=25a+45+2b=0\)・・・②
①②を解いて、\(a=-1\) \(b=-10\)
これは \(a<0\)を満たす。
これは \(a<0\)を満たす。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。