2次不等式を満たす整数に関連する問題を見ていきます。
(問題1)
\(x\)についての不等式 \(x^2-(a+1)x+a<0\)、\(3x^2+2x-1>0\)を同時に満たす整数\(x\)がちょうど3つ存在するような定数\(a\)の値の範囲を定めよ。
連立不等式です。まず両方をそれぞれ解いてみます。
(解答)
\(3x^2+2x-1>0\) より \((x+1)(3x-1)>0\)
よって解は、\(x<-1\) または \(x>\displaystyle\frac{1}{3}\)・・・①
\(3x^2+2x-1>0\) より \((x+1)(3x-1)>0\)
よって解は、\(x<-1\) または \(x>\displaystyle\frac{1}{3}\)・・・①
\(x^2-(a+1)x+a<0\) より \((x-a)(x-1)<0\)
(1)\(a<1\)のとき 解は \(a<x<1\)・・・②
(2)\(a=1\)のとき 解はなし
(3)\(a>1\)のとき 解は \(1<x<a\)・・・③
(1)\(a<1\)のとき 解は \(a<x<1\)・・・②
(2)\(a=1\)のとき 解はなし
(3)\(a>1\)のとき 解は \(1<x<a\)・・・③
ゆえに題を満たす条件は (1)(3)の場合である。
(1)\(a<1\)のとき
3つの整数\(x\)は \(x=-2,-3,-4\)
求める\(a\)の範囲は \(-5≦a<-4\)
3つの整数\(x\)は \(x=-2,-3,-4\)
求める\(a\)の範囲は \(-5≦a<-4\)
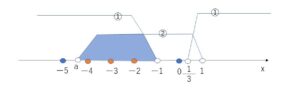
境目 \(a=-5,-4\) に注意してください。\(a=-5\) のときは、①②を満たす解が \(-5<x<-1\) となり、ちゃんと整数解は3つです。\(a=-4\)のときは \(-4<x<-1\) となり 整数解は \(x=-3,-2\) の2つとなり不適です。次の(3)の場合も同様に検討します。
(3)\(a>1\)のとき
3つの整数\(x\)は \(x=2,3,4\)
求める\(a\)の範囲は \(4<a≦5\)
3つの整数\(x\)は \(x=2,3,4\)
求める\(a\)の範囲は \(4<a≦5\)
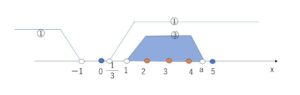
以上から、\(-5≦a<-4\) または \(4<a≦5\)
(問題2)
\(2x^2-3x+a<0\)を満たす整数\(x\)がちょうど4個存在するような定数\(a\)の範囲を求めよ。
\(2x^2-3x+a<0\)を満たす整数\(x\)がちょうど4個存在するような定数\(a\)の範囲を求めよ。
因数分解できそうにないので、グラフを用いて考えます。
\(f(x)=2x^2-3x+a\) とおく。
\(f(x)=2(x-\displaystyle\frac{3}{4})^2-\displaystyle\frac{9}{8}+a\) で
軸が\(x=\displaystyle\frac{3}{4}\)より、4つの整数解は、\(x=-1,0,1,2\) グラフより条件は
\(f(x)=2(x-\displaystyle\frac{3}{4})^2-\displaystyle\frac{9}{8}+a\) で
軸が\(x=\displaystyle\frac{3}{4}\)より、4つの整数解は、\(x=-1,0,1,2\) グラフより条件は
\(f(-2)=14+a≧0\)
\(f(-1)=5+a<0\)
\(f(2)=2+a<0\)
\(f(3)=9+a≧0\)
\(f(-1)=5+a<0\)
\(f(2)=2+a<0\)
\(f(3)=9+a≧0\)
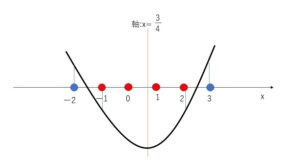
\(f(-2)\)と\(f(3)\)については\(0\)でも構いません。仮に両方\(0\)(あり得ませんが)とすると,解は \(-2<x<3\) となり、整数解は4つになります。
以上より、 \(-9≦a<-5\)
以上になります。お疲れさまでした。
ここまで読んで頂きありがとうございました。
ここまで読んで頂きありがとうございました。