本題に入る前に、2次関数の解の存在範囲について重要な性質を紹介します。
\(f(x)=ax^2+bx+c\) (ただし\(a≠0\))で \(p<q\)とすると、2次方程式
\(f(x)=ax^2+bx+c=0\) は \(f(p)\)と\(f(q)\)が異符号、つまり \(f(p)f(q)<0\) ならば \(p<x<q\)の範囲にただ1つの重解ではない実数解を1つもつ。
\(f(x)=ax^2+bx+c=0\) は \(f(p)\)と\(f(q)\)が異符号、つまり \(f(p)f(q)<0\) ならば \(p<x<q\)の範囲にただ1つの重解ではない実数解を1つもつ。
まず、\(a>0\)の場合を考える。
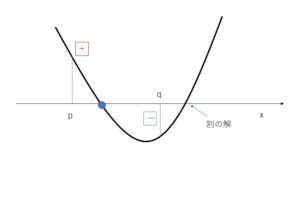
①\(f(p)>0\) かつ \(f(q)<0\) のとき
①\(f(p)>0\) かつ \(f(q)<0\) のとき
\(p\)から\(q\)まで\(x\)の値が変わるとき、\(f(x)\)の符号は正から負に変わるので、\(p\)から\(q\)の間のどこかで\(f(x)=0\)となる\(x\)が存在することになります。
よって、放物線\(f(x)\)はその形状から\(p<x<q\)の範囲で\(x\)軸とただ1点で交わり、\(p<x<q\)の範囲に\(f(x)=0\)の解が存在することになります。またもう1つの解は別の範囲に存在するので\(p<x<q\)の範囲にある解は重解ではありません。
よって、放物線\(f(x)\)はその形状から\(p<x<q\)の範囲で\(x\)軸とただ1点で交わり、\(p<x<q\)の範囲に\(f(x)=0\)の解が存在することになります。またもう1つの解は別の範囲に存在するので\(p<x<q\)の範囲にある解は重解ではありません。
②\(f(p)<0\) かつ \(f(q)>0\) のとき
\(p\)から\(q\)まで\(x\)の値が変わるとき、\(f(x)\)の符号が負から正に変わる以外①と同様です。
\(p\)から\(q\)まで\(x\)の値が変わるとき、\(f(x)\)の符号が負から正に変わる以外①と同様です。
\(a<0\)の場合も全く同じように考えることができます。
似たような話が数Ⅱや数Ⅲで出てきますが、数Ⅰではひとまずこれくらいにしておきます。
それでは本題に入りましょう。
(問題)
2次方程式 \(ax^2-2(a-5)x+3a-15=0\) の1つの解が\(-5\)と\(0\)の間にあり、他の解が\(1\)と\(2\)の間にあるとき、定数\(a\)の値の範囲を求めよ。
\(a=0\)の時は直線なので条件に合わないのは分かると思います。
また、2次の係数\(a\)の正負で上に凸か下に凸かグラフの形状が変わりますが、どちらの場合も求める条件は同じなので場合分けはしなくてもよいです。
また、2次の係数\(a\)の正負で上に凸か下に凸かグラフの形状が変わりますが、どちらの場合も求める条件は同じなので場合分けはしなくてもよいです。
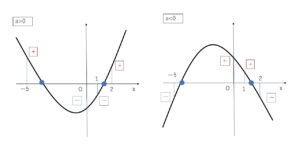
\(f(-5)f(0)<0\)かつ\(f(1)f(2)<0\)・・・①とすると
例えば左図では、\(f(-5)>0\)かつ\(f(0)<0\)かつ\(f(1)>0\)かつ\(f(2)<0\)(①を満たす)といったあり得ない条件も求まりそうと考える方もいるかもしれませんが、これらは数式処理で自動的に除かれます。(そもそもあり得ない条件は結果として出てきません)
例えば左図では、\(f(-5)>0\)かつ\(f(0)<0\)かつ\(f(1)>0\)かつ\(f(2)<0\)(①を満たす)といったあり得ない条件も求まりそうと考える方もいるかもしれませんが、これらは数式処理で自動的に除かれます。(そもそもあり得ない条件は結果として出てきません)
(解答)
\(f(x)=ax^2-2(a-5)x+3a-15\) (\(a≠0\)) とおくと題意を満たす条件は
\(f(-5)f(0)<0\) かつ \(f(1)f(2)<0\) つまり
\(f(x)=ax^2-2(a-5)x+3a-15\) (\(a≠0\)) とおくと題意を満たす条件は
\(f(-5)f(0)<0\) かつ \(f(1)f(2)<0\) つまり
\((38a-65)(3a-15)<0\) かつ \((2a-5)(3a+5)<0\)
よって \(\displaystyle\frac{65}{38}<a<5\) かつ \(-\displaystyle\frac{5}{3}<a<\displaystyle\frac{5}{2}\)
よって \(\displaystyle\frac{65}{38}<a<5\) かつ \(-\displaystyle\frac{5}{3}<a<\displaystyle\frac{5}{2}\)
ゆえに、\(\displaystyle\frac{65}{38}<a<\displaystyle\frac{5}{2}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
ここまで見て頂きありがとうございました。