文字定数を含む2次方程式の解の個数の問題を解いていきます。定数分離という手法を使ってグラフを利用して解いてみます。
(問題)
\(f(x)=|x^2+2x-3|+2x+6\)、\(g(x)=2x+a\) (\(a\)は定数) とする。
\(y=f(x)\) のグラフと \(y=g(x)\)のグラフの共有点の個数を求めよ。
そのまま \(y=f(x)\) と \(y=g(x)\) のグラフを書くと大変そうなので、
\(f(x)=g(x)\)を変形し、左辺と右辺を簡単な式にして、共有点の個数=解の個数という性質を利用します。その際に左辺と右辺を片方が\(x\)のみの式、もう一方を\(a\)のみの式にします。
\(f(x)=g(x)\)を変形し、左辺と右辺を簡単な式にして、共有点の個数=解の個数という性質を利用します。その際に左辺と右辺を片方が\(x\)のみの式、もう一方を\(a\)のみの式にします。
(解答)
2つのグラフの共有点の個数は、方程式 \(|x^2+2x-3|+2x+6=2x+a\)
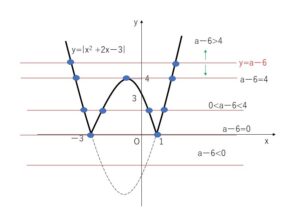
つまり \(|x^2+2x-3|=a-6\) の解の個数に等しい。よって \(y=|x^2+2x-3|\)のグラフ と \(x\)軸に平行な直線 \(y=a-6\) の共有点の個数に一致する。
左辺の \(y=|x^2+2x-3|\) という関数は\(a\)が含まれていないので、\(xy\)平面に固定させて描くことができます。これがポイントで、定数\(a\)を\(x\)と分離させた結果、グラフを固定させることができたわけです。あとは右辺は\(a\)の値の変化で\(x\)軸に平行な直線が上下するだけなので、上下させたときにどう共有点の個数が変化するか調べます。
\(x^2+2x-3=(x+3)(x-1)\) なので
\(x≦-3\) または \(x≧1\)のとき
\(y=|x^2+2x-3|=x^2+2x-3\)
\(-3<x<1\) のとき
\(y=|x^2+2x-3|=-x^2-2x+3\)
よりグラフを書くと下図となる。よって \(a-6=0,4\) つまり \(a=6,10\) を境目にして場合分けすると、求める共有点の個数は
\(a<6\) のとき 0個
\(a=6\) のとき 2個
\(6<a<10\) のとき 4個
\(a=10\) のとき 3個
\(a>10\) のとき 2個
以上になります。お疲れさまでした。
ここまで読んで頂きありがとうございました。
→高校数学TOP next→2つの放物線の共有点 back→絶対値を含む2次方程式・不等式