今回の極方程式で表された曲線は、カージオイドとリマソンです。
・カージオイド
\(r=a(1+\cosθ)\)・・・①
で表される曲線をカージオイド(心臓形)と呼びます。カージオイドを極方程式のまま描く方法は
\(r=a+a\cosθ\)
とみて、\(r=a\cosθ\) が円を描くことを利用します。
\(a=2\) として
\(r=2+2\cosθ\)・・・②
の曲線の概形を調べてみます。
\(2+2\cos(θ+2π)=2+2\cosθ\) だから、\(0≦θ≦2π\) の範囲で考えれば十分です。
\(r=2\cosθ\)・・・③ は、中心 \((1,0)\) である半径\(1\)の円を描き、\(0≦θ≦2π\) の範囲で円を2周します。特に③は \(\displaystyle\frac{π}{2}≦θ≦\displaystyle\frac{3π}{2}\) では \(r≦0\) になることに注意すると、②を描くには
(i)\(0≦θ≦\displaystyle\frac{π}{2},\ \displaystyle\frac{3π}{2}≦θ≦2π\) では、極から円まで動かしてさらに\(2\)だけ増やす。
(ii)\(\displaystyle\frac{π}{2}≦θ≦\displaystyle\frac{3π}{2}\) では、極から円まで進み、逆方向に\(2\)だけ動かす。
とすればよいので、グラフの概形は次のようになります。(始線について対称となる。これは \(2+2\cos(-θ)=2+\cosθ\) からも分かる)
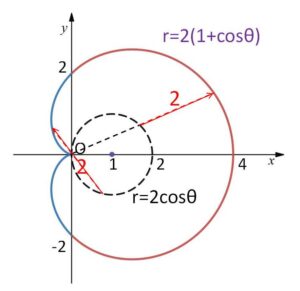
なお②自体は \(r≧0\) なので、②だけで考える場合には\(θ\)によって\(π\)移動(\(180°\)回転)はしないことになります。
ところでカージオイド①を媒介変数表示にすると
\(\begin{eqnarray} \left\{ \begin{array}{l} x=a(1+\cosθ) \cosθ \\ y = a(1+\cosθ)\sinθ \end{array} \right. \end{eqnarray}\)
となり、この式より曲線の概形を描くことも可能です。
また、カージオイドは外サイクロイド(固定された円に外接しながら動く円の円周上の1点の軌跡)の特殊例(2円の半径が同じ)で定義される場合もあります。この場合2円の半径を\(\displaystyle\frac{a}{2}\)、固定円の中心 \((\displaystyle\frac{a}{2},0)\)、動かす円の中心と円周上の点\(P\)の初期位置を、\((\displaystyle\frac{3a}{2},0)\)、\(P(2a,0)\) として、ベクトルを利用すると
\(\overrightarrow{OP}=a(1+\cosθ)(\cosθ,\sinθ)\)
となるので、曲線は一致します。
・リマソン
\(r=a+b\cosθ\)・・・(1)
で表される曲線をリマソン(蝸牛形)と呼びます。\(a=b\) のときカージオイドになるので、リマソンの特殊例がカージオイドになるとみることもできます。
リマソンの概形を描く方法は、カージオイドの場合と同じで 円 \(r=b\cosθ\) を基準として\(a\)だけ動かすという手法をとります。\(a,b\)の大小で\(r\)が常に一定の符号を取り続ける場合と、正負のどちらもとる場合があるので、\(a,b\)の大小によって形状が若干異なります。
(ア)\(a>b\) のとき
\(a=3\)、\(b=2\) として
\(r=3+2\cosθ\)・・・(2)
常に \(r>0\) となり、カージオイドとほぼ同様になるので、概形は次の通り。
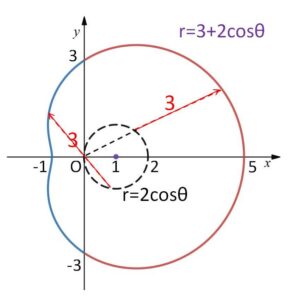
(イ)\(a<b\) のとき
\(a=1\)、\(b=2\) として
\(r=1+2\cosθ\)・・・(3)
今度は、\(\displaystyle\frac{π}{2}≦θ≦\displaystyle\frac{3π}{2}\) で、\(r≦0\) となる場合(\(\displaystyle\frac{2π}{3}≦θ≦\displaystyle\frac{4π}{3}\)) があるため、内側にもループを作ることになります。
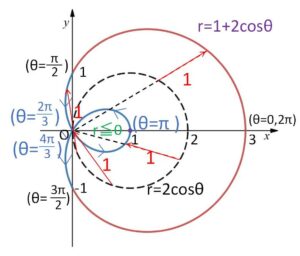
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→極座標を利用する証明・最大最小問題 back→極方程式と曲線の概形②