(定理)
\(X\)が二項分布 \(B(n,p)\) に従うとき、\(n\)が十分大きい値ならば、\(X\)は近似的に正規分布\(N(np,np(1-p))\) に従う。
(証明)
二項分布の期待値と分散は
\(E(X)=np\)、\(V(X)=np(1-p)\)
\(X\)を標準化すると
\(Z=\displaystyle\frac{X-np}{\sqrt{np(1-p)}}\)
よって、\(Z\)が標準正規分布に従うことを示せばよい。
証明には中心極限定理を利用します。中心極限定理は標本平均
\(\overline{X}=\displaystyle\frac{X_1+X_2+\cdots+X_n}{n}\)
が\(n\)が十分大きいとき\(\overline{X}\)が正規分布に従うという定理ですが、二項分布の確率変数\(X\)は確率\(p\)で起きる事象の総回数なので \(X_k=0,1\) (それぞれ確率\(1-p,p\))という値をとる\(X_k\)を用いて
\(X=X_1+X_2+\cdots+X_n\)
で表され、\(\overline{X}\)と\(\displaystyle\frac{1}{n}\)倍だけズレがあります。そこで標準化の分数式の分母分子に同じ式を掛けて調整することで証明を完了させます。
\(X_1,X_2,\cdots,X_n\)はすべて同じ分布(母集団分布)に従いますが、この母集団分布は、値\(0,1\) を\(1-p,p\) でとるだけという単純な分布になっていることに注意して下さい。つまりここでいう母集団分布は \(n=1\) の場合の二項分布です。
\(1\)回の試行で確率\(p\)で起きる事象を\(A\)として、\(n\)回試行を繰り返したとき
「\(X_k\)を、\(k\)回目の試行で\(A\)が起きれば \(X_k=1\)、起きなければ \(X_k=0\) という値をとる確率変数」とすれば、\(X\)は\(n\)回試行したときの\(A\)が起きる総回数だから
\(X=X_1+X_2+\cdots+X_n\)
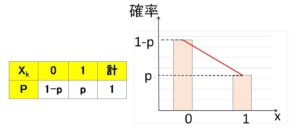
\(X_k\)を大きさ\(1\)の標本の確率変数とみると、どの\(X_k\)も上記確率分布(母集団分布)に従い、この母集団分布の期待値と標準偏差は
\(m=0\cdot(1-p)+1\cdot p=p\)
\(σ^2=0^2\cdot(1-p)+1^2\cdot p-p^2=p(1-p)\)
であり、\(n\)が十分大きいので中心極限定理より標本平均
\(\overline{X}=\displaystyle\frac{X_1+X_2+\cdots+X_n}{n}\)
は、近似的に正規分布 \(N(p,\displaystyle\frac{p(1-p)}{n})\) に従う。
よって
\(Z’=\displaystyle\frac{\overline{X}-p}{\sqrt{\displaystyle\frac{p(1-p)}{n}}}\)
は標準正規分布に従い、\(Z’\)を変形すると
\(Z’=\displaystyle\frac{\displaystyle\frac{X_1+X_2+\cdots+X_n}{n}-p}{\sqrt{\displaystyle\frac{p(1-p)}{n}}}\)
\(=\displaystyle\frac{(X_1+X_2+\cdots+X_n)-np}{\sqrt{np(1-p)}}\)
\(=\displaystyle\frac{X-np}{\sqrt{np(1-p)}}\)
となるので、\(Z\)(\(Z’\)と同じ)が標準正規分布に従うことが示され、題意は証明された。