直角三角形における三角比の定義においては\(90°\)である角以外の角、つまり鋭角について考えたので、角の大きさ\(θ\)とすると、 \(0°<θ<90°\)での範囲でしか三角比の値は与えられません。しかし、角度には\(150°\)や\(360°\)など,この範囲外のものもあるので直角三角形の定義を改めて、さまざまな角度に対応できるように定義し直します。定義し直す準備として、座標平面と半径\(r\) (\(r>0\))の円を用意します。
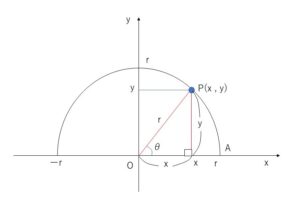
まず、座標平面上に原点\(O\)を中心とする半径\(r\)の半円を書き、この半円と\(x\)軸の正の部分との交点を\(A\)とします。まず、\(θ\)を鋭角としてこの半円の周上に\(\angle AOP=θ\)となる点\(P\)をとり、点\(P\)の座標を\((x,y)\)とします。このとき直角三角形の三角比の定義より次のことが成り立ちます。
\(\sinθ=\displaystyle\frac{y}{r}\), \(\cosθ=\displaystyle\frac{x}{r}\), \(\tanθ=\displaystyle\frac{y}{x}\)
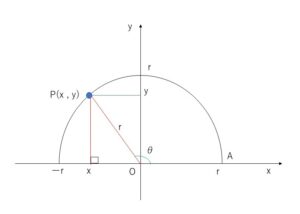
これをそのまま他の角度についても当てはめてしまおうというのが新しい定義の内容です。\(0°≦θ≦180°\)において三角比を次のように定義します。先ほど考えた半円上に\(\angle AOP=θ\)となる点\(P(x,y)\)をとるとき
\(\sinθ=\displaystyle\frac{y}{r}\), \(\cosθ=\displaystyle\frac{x}{r}\), \(\tanθ=\displaystyle\frac{y}{x}\)
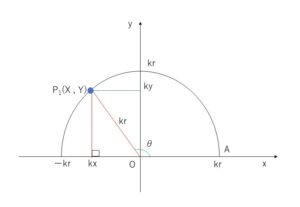
\(\angle AOP_1=θ\)となる点\(P_1(X,Y)\)をとるとき、図形の相似から\((X,Y)=(kx,ky)\)となる。よって\(\sinθ=\displaystyle\frac{ky}{kr}=\displaystyle\frac{y}{r}\), \(\cosθ=\displaystyle\frac{kx}{kr}=\displaystyle\frac{x}{r}\), \(\tanθ=\displaystyle\frac{ky}{kx}=\displaystyle\frac{y}{x}\)となり、半径を変化させても三角比の値は変わらない。
具体的に鋭角ではない三角比の値を求めてみましょう。
(例題1)
\(\sin120°,\cos120°,\tan120°\) を求めよ。
(解答)
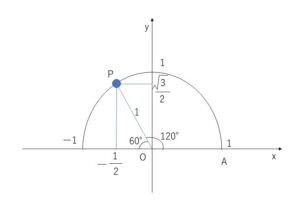
単位円上に \(\angle AOP=120°\) となる点\(P\)をとり\(P\)の座標を求める。
\(P\)の座標は、\((-\displaystyle\frac{1}{2},\displaystyle\frac{\sqrt{3}}{2})\) となり、
\(\sin120°=\displaystyle\frac{y}{1}=\displaystyle\frac{\sqrt{3}}{2}\)
\(\cos120°=\displaystyle\frac{x}{1}=-\displaystyle\frac{1}{2}\)
\(\tan120°=\displaystyle\frac{y}{x}\)\(=\displaystyle\frac{\sqrt{3}}{2}÷(-\displaystyle\frac{1}{2})=-\sqrt{3}\)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。