未知数の角の三角比を含む不等式、三角不等式の解法について考えていきます。
(問題1)
\(0°≦θ≦180°\) のとき、\(\sinθ≧\displaystyle\frac{1}{2}\) を解け。
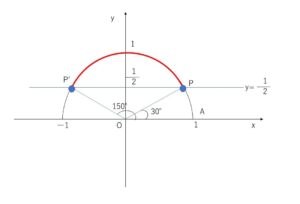
単位円周上で、\(y\)座標が\(\displaystyle\frac{1}{2}\) 以上の点に対応する\(θ\)の範囲を求めればよいので、まず境目である\(\sinθ=\displaystyle\frac{1}{2}\)を満たす\(θ\)を求め、あとは図より不等式を満たす\(θ\)の範囲を求めます。
(解答)
\(y=\displaystyle\frac{1}{2}\) と単位円の交点は\(P,P’\)の2点で、\(\angle AOP=30°\), \(\angle AOP’=150°\)
\(y\)座標が\(\displaystyle\frac{1}{2}\)以上の点は、単位円周上の\(P\)から\(P’\)の間にあるので、
求める解は \(30°≦θ≦150°\)
\(y=\displaystyle\frac{1}{2}\) と単位円の交点は\(P,P’\)の2点で、\(\angle AOP=30°\), \(\angle AOP’=150°\)
\(y\)座標が\(\displaystyle\frac{1}{2}\)以上の点は、単位円周上の\(P\)から\(P’\)の間にあるので、
求める解は \(30°≦θ≦150°\)
(問題2)
\(0°≦θ≦180°\) のとき、 \(2\cosθ+\sqrt{3}>0\) を解け。
\(0°≦θ≦180°\) のとき、 \(2\cosθ+\sqrt{3}>0\) を解け。
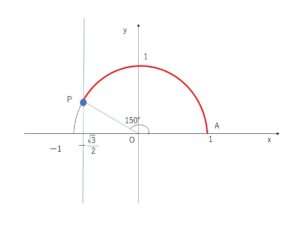
\(\cosθ\)は単位円周上の点\(P\)の\(x\)座標です。
与式から、 \(\cosθ>-\displaystyle\frac{\sqrt{3}}{2}\) なので、\(x\)座標が \(-\displaystyle\frac{\sqrt{3}}{2}\) より大きい単位円周上の点に対応する\(θ\)を求めます。
与式から、 \(\cosθ>-\displaystyle\frac{\sqrt{3}}{2}\) なので、\(x\)座標が \(-\displaystyle\frac{\sqrt{3}}{2}\) より大きい単位円周上の点に対応する\(θ\)を求めます。
(解答)
与式から、 \(\cosθ>-\displaystyle\frac{\sqrt{3}}{2}\)
\(\cosθ=-\displaystyle\frac{\sqrt{3}}{2}\) を解くと、 \(θ=150°\)
与式から、 \(\cosθ>-\displaystyle\frac{\sqrt{3}}{2}\)
\(\cosθ=-\displaystyle\frac{\sqrt{3}}{2}\) を解くと、 \(θ=150°\)
よって図より不等式を満たす\(θ\)は
\(0°≦θ<150°\)
\(0°≦θ<150°\)
(問題3)
\(0°≦θ≦180°\) のとき、 \(\tanθ≦1\) を解け。
単位円周上の点\(P\)と原点を結ぶ直線は,\(T(1,\tanθ)\)を通るので、\(T\)の\(y\)座標が1より小さくなる点\(P\)に対応する\(θ\)を求めます。\(θ=90°\)では\(\tanθ\)は定義されないことに注意します。
(解答)
\(\tanθ=1\) を解くと、\(θ=45°\)
\(\tanθ\)は、単位円周上の点\(P\)と原点\(O\)を結ぶ直線の\(x=1\)での\(y\)座標なので、この\(y\)座標が\(1\)以下となる、点\(P\)に対応する\(θ\)を求める。
\(\tanθ=1\) を解くと、\(θ=45°\)
\(\tanθ\)は、単位円周上の点\(P\)と原点\(O\)を結ぶ直線の\(x=1\)での\(y\)座標なので、この\(y\)座標が\(1\)以下となる、点\(P\)に対応する\(θ\)を求める。
図より、\(0°≦θ≦45°\), \(90°<θ≦180°\)
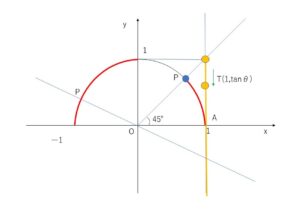
\(90°<θ≦180°\) の範囲では、\(\tanθ≦0\) なので、この部分はまるまる解となります。
・三角比の2次不等式
(問題)
\(0°≦θ≦180°\) のとき、不等式 \(8\cos^2θ-6\sinθ<3\) を解け。
途中までは\(x\)の2次不等式と同様にして解いていきます。\(\sinθ\)や\(\cosθ\) の値の範囲に注意です。
(解答)
与式より、\(8(1-\sin^2θ)-6\sinθ-3<0\)
整理して
\(8\sin^2θ+6\sinθ-5>0\)
\((4\sinθ+5)(2\sinθ-1)>0\)
ここで、\(0°≦θ≦180°\) のとき\(\sinθ≧0\) だから \(4\sinθ+5>0\)より
\(2\sinθ-1>0\)
よって \(\sinθ>\displaystyle\frac{1}{2}\)・・・①
与式より、\(8(1-\sin^2θ)-6\sinθ-3<0\)
整理して
\(8\sin^2θ+6\sinθ-5>0\)
\((4\sinθ+5)(2\sinθ-1)>0\)
ここで、\(0°≦θ≦180°\) のとき\(\sinθ≧0\) だから \(4\sinθ+5>0\)より
\(2\sinθ-1>0\)
よって \(\sinθ>\displaystyle\frac{1}{2}\)・・・①
①を\(0°≦θ≦180°\) の範囲で解くと
\(30°<θ<150°\)
\(30°<θ<150°\)

以上です。お疲れさまでした。
ここまで見て頂きありがとうございました。